Petit défi de proba
Olympiades mathématiques, énigmes et défis

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Juin 2015, 21:16
par Ben314 » 11 Juin 2015, 21:16
Autre méthode axée sur le fait qu'un un dérangement de {1..n}, c'est une permutation qui se décompose en cycles à supports disjoints de longueur au moins égal à 2.
Donc un dérangement s'écrit de façon unique comme un cycle de longueur j>=2 "commençant" par 1 composé avec un dérangement des n-j autres éléments ce qui nous dit que, pour tout

,
!}{(n-j)!}d_{n-j}<br />=(n-1)!\sum_{k=0}^{n-2}\frac{d_k}{k!}<br />=(n-1)!\Big(\frac{d_{n-2}}{(n-2)!}+\sum_{k=0}^{n-3}\frac{d_k}{k!}\Big)<br />=(n-1)!\Big(\frac{d_{n-2}}{(n-2)!}+\frac{d_{n-1}}{(n-2)!}\Big)<br />=\frac{n!}{n}\Big(\frac{d_{n-2}}{(n-2)!}+(n-1)\frac{d_{n-1}}{(n-1)!}\Big))
d'où, si on pose
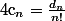
, on a
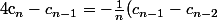<br />=+\frac{1}{n(n-1)}(c_{n-2}-c_{n-3})<br />=\cdots<br />=\frac{(-1)^{n-1}}{n!}(c_1-c_0)<br />=\frac{(-1)^n}{n!})
Ce qui signifie que
^n}{n!})
et on en déduit que
^k}{k!})
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 12 Juin 2015, 07:54
par nodjim » 12 Juin 2015, 07:54
Qu'on trouve 1/e ou autre chose, ce n'est pas très spectaculaire. On pourrait à la limite se demander si ce résultat est contre intuitif, mais ici l'intuition n'est pas évidente du tout: pour n qui tend vers l'infini, on a une infinité d'essais dont la réussite de chacun est proche de 0, ce qui laisse beaucoup d'interrogation sur la valeur finale entre 0 et 1....

-
Darkwolftech
- Membre Relatif
- Messages: 140
- Enregistré le: 11 Jan 2014, 18:42
-
 par Darkwolftech » 12 Juin 2015, 15:32
par Darkwolftech » 12 Juin 2015, 15:32
nodjim a écrit:Qu'on trouve 1/e ou autre chose, ce n'est pas très spectaculaire.
Ah, ben désolé pour ma naïveté et mon manque de recul toussa toussa, mais moi ça m'impressionne :lol3:
-
Rouvire
- Membre Naturel
- Messages: 35
- Enregistré le: 02 Fév 2014, 14:16
-
 par Rouvire » 12 Juin 2015, 18:47
par Rouvire » 12 Juin 2015, 18:47
Bonjour,
J'avais posté le 8/2/2014 quelque chose de semblable dans le Café:
"J'ai un jeu de n cartes. Elles sont numérotées de 1 à n. Je les bats et pose le paquet face cachée sur une table.
Je tire la 1ère carte du dessus et la repose à coté du paquet face découverte. Si c'est la carte n°1 j'ai perdu ma réussite, sinon je continue, je tire la carte du dessus du paquet et la repose face découverte sur la 1ère que je viens de tirer. Si c'est la carte n°2 j'ai perdu, sinon je continue et ainsi de suite. Je gagne ma réussite si j'arrive à retourner ainsi tout le paquet et que la dernière carte retournée n'est pas la n°n."
Ben314 m'avait déjà indiqué que la probabilité de réussir était le rapport du nombre de dérangements sur factoriel n (n!) et qu'il tendait bien vers 1/e quand n allait vers l'infini.
Je me posais la question quand je faisais le l'"aller-retour". C.a.d, quand après avoir gagné en partant du paquet face cachée on repartait du même paquet qui cette fois était face découverte et je pensais que la probabilité pour n infini tendait vers 1/e^2
==> je pense maintenant que si on a A paquets de n infini cartes numérotées de 1 à n (c'est pas très possible) et que dans ces A paquets aucune carte n'est à la même position (par exemple si la carte n°5 du 1er paquet est en position 10 la carte n°5 du 4ème paquet ne sera pas en position 10), alors si je prends un autre paquet de n infini carte, la probabilité que dans ce nouveau paquet aucune carte ne soit dans la même position qu'une autre des A autres paquets devrait aller vers 1/e^A
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités