Grand théoreme de fermat

[lapras]

Bonsoir.
Considérons un nombre p premier tel que 2p+1 soit aussi premier.
Montrer que l'équation n'a pas de solutions non triviales avec p premier avec xyz.

Lapras :we:

[acoustica]

Bonsoir.
Considérons un nombre p premier tel que 2p+1 soit aussi premier.
Montrer que l'équation n'a pas de solutions non triviales pour p premier avec xyz.

Lapras :we:

C'est le théorème de Sophie-Germain?

[lapras]

Oui comment le sais tu ?

[acoustica]

Oui comment le sais tu ?

Il y a quelques mois, je m'étais pris d'une passion subite pour le théorème de Fermat dans des cas particuliers! (Depuis, j'ai quand même eu le temps de passer à autre chose) :happy2:

[lapras]

Bien ! Et as tu démontré ce cas là ?

[acoustica]

Bien ! Et as tu démontré ce cas là ?

Non, j'ai lu la démonstration!! On va dire que le cas n=4 est faisable mais difficile, le cas n=3 est carrément balèze: il est sur Wiki ou dans le Tanjente Hors Série sur Euler (tu l'as peut-être déjà, sinon, je peux t'assurer que tu es servi en belles démonstrations et arithmétique. Il y a certaines démo qui donnent les larmes aux yeux... :we: ). Théorème de Sophie Germain, je ne me souvient plus, mais je crois qu'il est aussi sur Wiki. Je vais vérifier.

[acoustica]

Yep:
http://fr.wikipedia.org/wiki/D%C3%A9monstrations_du_dernier_th%C3%A9or%C3%A8me_de_Fermat

[lapras]

Le cas n=4 est n'est pas difficile (ce n'est pas du niveau olympiades).
Le cas n=3 est moins facile mais faisable quand on a un bagage minimum de théorie algébrique des nombres.
Le cas n=5 est déjà plus baleze mais compréhensible avec ces outils.
Le théoreme de sophie germain est équivalent au cas n=4 en difficulté je pense.

[acoustica]

Le cas n=4 est quand même classé trois étoiles dans le poly d'arithmétique des olympiades...mais je suis d'accord, il y en a des beaucoup plus durs classés plus simples.

[lapras]

Je ne savais pas ! Disons qu'il ne demande pas d'astuces à part connaître les triplets pythégoriciens.

[acoustica]

Je ne savais pas ! Disons qu'il ne demande pas d'astuces à part connaître les triplets pythégoriciens.

Oui c'est vrai que ce n'est pas le plus technique. Mais la démo est belle.

[lapras]

Sinon, pour ceux qui souhaitent chercher seuls l'exercice, même si une démo est sur wiki ca serait bien de poster la votre !

[ThSQ]

C'est le théorème de Sophie-Germain?

D'ailleurs les nombres premiers p tels que 2p+1 est aussi premier sont appelés en son honneur.

[lapras]

Je viens de prouver une variante.
Montrer que l'équation
n'a pas de solutions non triviales avec p premier tel que 2p+1 est aussi premier et p ne divise pas y.

Lapras :happy2:

[yos]

Il me semble que Sophie Germain, c'est moins fort que ça. C'est seulement le premier cas du th. Fermat :
, p ne divise pas et p, 2p+1 premiers , mais c'est peut-être ça que tu appelles une solution triviale.

[lapras]

Oui tu as raison je modifie.

[lapras]

Enoncé :
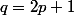
Soit premier impair tel que soit aussi premier.
On suppose ne divise pas et que ne divise pas .
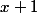
Alors l'équation n'a pas de solutions non triviales.

Démonstration :

Lemme 1 :
Soit un entier tel que ne divise pas .
Alors ou

Preuve :
(fermat)
donc q divise d'où le résultat.


Lemme 2 :
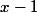
Si ne divise pas , alors


Preuve :

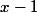
or chacun des termes entre paranthèse est divisible par (factorisation )
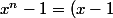donc
divise
donc .
D'où le résultat.


Lemme 3:
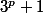
n'est jamais divisible par .

Preuve :
Notons que est divisible par q (fermat).
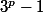
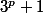
donc ou est divisible par q.
Montrons que 3 est un carré modulo q.
D'apres la loie de réciprocité quadratique,
3 est un carré modulo q ssi q n'est pas un carré modulo 3. Ce qui est vrai car
dooc /

donc
(fermat)
donc

donc q divise
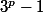
donc q ne divise pas .
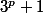
D'ou le résultat.



Démontrons maintenant le résultat principal.

L'équation se réécrit :

Le lemme 2 donne l'existence d'entiers a et b tels que :


et ou .
D'apres le lemme 1, ou
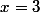
Cas 1 : [q]
alors

donc
ou
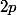
donne ce qui est impossible car l'ordre de modulo divise et on vérifie qu'il est égal à p ou 2p. Or et ne divise pas , donc l'ordre ne divise pas ce qui est absurde.

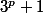
Le deuxieme cas donne divise ce qui est impossible par le lemme 3.

Cas 2 :
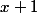
alors divise impossible par hypothèse.


D'où le résultat.