Fonction continue bornée
22 messages
- Page 1 sur 2 - 1, 2
fonction continue bornée
Salut à tous !
pour les lycéens, je propose de démontrer l'équivalence suivante, facile mais intriguante :
Soit X un sous-ensemble de R. Montrer que les propositions suivantes sont équivalentes :
i) Toute fonction continue sur X est bornée
ii) Toute fonction continue et bornée sur X atteint ses bornes.
bon courage.
:happy3:
pour les lycéens, je propose de démontrer l'équivalence suivante, facile mais intriguante :
Soit X un sous-ensemble de R. Montrer que les propositions suivantes sont équivalentes :
i) Toute fonction continue sur X est bornée
ii) Toute fonction continue et bornée sur X atteint ses bornes.
bon courage.
:happy3:
Rebelle_ a écrit:B'soir =)
Alors, voyons si j'ai bien compris le problème ^^' En gros l'énoncé est le suivant.
Soitune fonction définie et continue sur
, on a
bornée sur
et
atteint ses bornes
et
.
C'est bien ça ou je me trompe ?
Salut !
Non, justement, bien que ça à un gros rapport avec ce théorème, ce n'est pas ce que je demande de montrer.
Edit : Attention cela dit, il y a des "non-sens" dans le théorème cité. "f([a,b]) atteint ses bornes" n'a pas vraiment de sens. C'est f qui est bornée et atteint ses bornes
Edit 2 : la résolution de l'exercice n'emploie pas ce théorème
Je vais formuler autrement, il faut montrer :
(sens direct) Si toutes les fonctions continues sur X sont bornées, alors elles atteignent toutes leurs bornes
(sens indirect) Si toute fonction continue sur X qui est bornée atteint ses bornes, alors toutes les fonctions continues sur X sont en fait bornées.
(sens direct) Si toutes les fonctions continues sur X sont bornées, alors elles atteignent toutes leurs bornes
(sens indirect) Si toute fonction continue sur X qui est bornée atteint ses bornes, alors toutes les fonctions continues sur X sont en fait bornées.
Qmath a écrit:C'est avec Bolzano Weirestrass que ça se fait non ?
Pour le sens indirecte : lhypothèse n'est elle pas équivalente a la conclusion ?
Non, rien d'aussi "compliqué" que Bolzano-Weierstrass, cela dit si tu as une preuve avec, ne t'en prive pas pour la donner.
Pour le sens indirect, pourquoi donc l'hypothèse serait-elle équivalente à la conclusion? Dans l'hypothèse, on a deux données sur f, qu'elle est continue et bornée. Dans la conclusion, on demande de montrer qu'alors l'hypothèse "bornée" est automatiquement vérifiée.
Qmath a écrit:Je parlais de cette preuve http://bkristof.free.fr/cours/Cours%20-%20Continuite.pdf (fin de page 7)
Non, comme Juliette, tu ne traites pas le bon énoncé !! Eh les jeunes, il faut se concentrer un peu :lol3:
Salut,
je me permet de réécrire l'énoncé différemment, peut-être qu'ils comprendront mieux cette fois (et j'espère moi-même ne pas m'être planté... lol)
Soit) l'ensemble des fonctions continues sur X.
l'ensemble des fonctions continues sur X.
Soit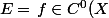 \, | \, f \, borne \, } \right)
Soit
Par construction, on voit que F c E c C°(X).
Il faut démontrer qu'il y a équivalence entre "E c F" et "C°(X) c E", donc équivalence entre "E = F" et "C°(X) = E"
Autrement dit,
Sens direct : si E=C°(X), alors E=F
Sens indirect : si E=F alors, E=C°(X)
je me permet de réécrire l'énoncé différemment, peut-être qu'ils comprendront mieux cette fois (et j'espère moi-même ne pas m'être planté... lol)
Soit
Soit
Soit
Par construction, on voit que F c E c C°(X).
Il faut démontrer qu'il y a équivalence entre "E c F" et "C°(X) c E", donc équivalence entre "E = F" et "C°(X) = E"
Autrement dit,
Sens direct : si E=C°(X), alors E=F
Sens indirect : si E=F alors, E=C°(X)
Pour le i) ==> ii) je connaissais la demo (d'ailleurs je croit qu'elle se trouve dans le pdf cite dans ce post)
pour le ii)==> i) :
Soit f(x) une fonction continue sur X .
Considérons la fonction= \frac{1}{|f(x)|+1}) .
.
F(x) est continue est bornée donc atteint ses bornes daprès ii)
On a donc \leq M)
Ce qui donne|+1 \leq \frac{1}{m})
| \leq \frac{1}{m}-1)
|f(x)| étant bornée f(x) est donc bornée.
CQFD
pour le ii)==> i) :
Soit f(x) une fonction continue sur X .
Considérons la fonction
F(x) est continue est bornée donc atteint ses bornes daprès ii)
On a donc
Ce qui donne
|f(x)| étant bornée f(x) est donc bornée.
CQFD
ii) => i)
Soit f une fonction continue, si on prend g(x) = arctan(f(x)), g est continue et bornée donc atteint ses bornes par ii). Donc soit M = Max (|g(x)|) ii)
Soit f une fonction continue bornée et soit M tel que pour tout x, |f(x)| < M.
Alors la fonction g(x) = tan (f(x)*pi/2M) est une fonction continue, donc bornée par un certain N, donc il existe M' = M* 2arctan(N)/pi < M tel que pour tout x, |f(x)| < M'.
A partir de là, on peut en déduire que f atteint ses bornes.
Soit f une fonction continue, si on prend g(x) = arctan(f(x)), g est continue et bornée donc atteint ses bornes par ii). Donc soit M = Max (|g(x)|) ii)
Soit f une fonction continue bornée et soit M tel que pour tout x, |f(x)| < M.
Alors la fonction g(x) = tan (f(x)*pi/2M) est une fonction continue, donc bornée par un certain N, donc il existe M' = M* 2arctan(N)/pi < M tel que pour tout x, |f(x)| < M'.
A partir de là, on peut en déduire que f atteint ses bornes.
Ah ! enfin des amateurs.
Arnaud > Non, pas de compacité dans l'air !
Qmath > Je ne vois pas la preuve de i) => ii) dans le pdf mais il faut dire que je n'ai fait que le survoler
Concernant ii)=>i) what if m ou M est nul?
Doraki > ii) => i) ok j'ai fait pareil, i) => ii) Ok aussi, mieux que ce que j'ai fait (considérer 1/(f-sup f), si sup f n'est pas atteint, cette fonction est continue mais non bornée).
Arnaud > Non, pas de compacité dans l'air !
Qmath > Je ne vois pas la preuve de i) => ii) dans le pdf mais il faut dire que je n'ai fait que le survoler
Concernant ii)=>i) what if m ou M est nul?
Doraki > ii) => i) ok j'ai fait pareil, i) => ii) Ok aussi, mieux que ce que j'ai fait (considérer 1/(f-sup f), si sup f n'est pas atteint, cette fonction est continue mais non bornée).
sens direct
On suppose que Toute fonction continue sur X est bornée
l'identite etant continue elles est donc bornee et X est une partie bornee
si x_n est une suite d'elements de X qui converge dans R vers x.
si x n'est pas dans X t -> 1/(t-x) est continue sur R\{x} et donc sur X, elle est donc bornee sur X.
et la suite des 1/(x_n-x) est bornee, ce qui est absurde.
donc x est dans X.
ce qui prouve que X est ferme et borne dans R il est compact et toute fonction continue sur X est bornee et atteint ses bornes.
Reciproque
Supposons que Toute fonction continue et bornée sur X atteint ses bornes.
en regardant t -> 1-exp(-|t|) elle est continue et bornee, elle atteint ses bornes donc X est bornee (sinon la borne sup est 1 et ne peut etre atteinte)
si x_n est une suite d'elements de X qui converge dans R vers x.
t -> exp(-(t-x)²) est continue et bornee, elle atteint donc ses bornes. ce qui implique que x est dans X. (sinon la suite des exp(-(x_n-x)²) va tendre vers 1 qui est le sup de la fonction sans que celui ci soit atteint).
on a la aussi un ferme borne de R donc un compact.
et toute fonction continue est bornee.
On suppose que Toute fonction continue sur X est bornée
l'identite etant continue elles est donc bornee et X est une partie bornee
si x_n est une suite d'elements de X qui converge dans R vers x.
si x n'est pas dans X t -> 1/(t-x) est continue sur R\{x} et donc sur X, elle est donc bornee sur X.
et la suite des 1/(x_n-x) est bornee, ce qui est absurde.
donc x est dans X.
ce qui prouve que X est ferme et borne dans R il est compact et toute fonction continue sur X est bornee et atteint ses bornes.
Reciproque
Supposons que Toute fonction continue et bornée sur X atteint ses bornes.
en regardant t -> 1-exp(-|t|) elle est continue et bornee, elle atteint ses bornes donc X est bornee (sinon la borne sup est 1 et ne peut etre atteinte)
si x_n est une suite d'elements de X qui converge dans R vers x.
t -> exp(-(t-x)²) est continue et bornee, elle atteint donc ses bornes. ce qui implique que x est dans X. (sinon la suite des exp(-(x_n-x)²) va tendre vers 1 qui est le sup de la fonction sans que celui ci soit atteint).
on a la aussi un ferme borne de R donc un compact.
et toute fonction continue est bornee.
Nightmare a écrit:
Qmath > Je ne vois pas la preuve de i) => ii) dans le pdf mais il faut dire que je n'ai fait que le survoler
Concernant ii)=>i) what if m ou M est nul?
i)==>ii)
Jétudie la fonction
Supposons que M ne soit pas atteint alors F(x) qui est continue est bornée. Soit M' sa borne superieur.
On a
[TEX]f(x) i) J'ai du mal a voir comment m ou M (surtout ) peuvent etre nuls. Peux- tu donner un exemple ?
EDit: En effet m peut etre nul ...
22 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
