déterminer toutes les fonctions
[Analyse] équation fonctionelle
15 messages
- Page 1 sur 1
pas très bon en calcul hier soir j'avais f(x) = -x qui me semble bon
et comme je suis nul en calcul j'avais aussi f(x) = ax qui est faux.
Sinon, je n'ai pas l'habitude de résoudre ces trucs là.
Alors je commencerai doucement,
en prenant quelques valeurs comme
x=0
f(0) = f(y)x f(0)
pour tout y, de là à penser que f(0) = 0 !
alors
pour y = 0
f(xf(x)) = x² je sais pas si c'est utile
avec x=1
f(f(y+1)) = f(y)f(1) +1
...
jamais bossé ces techniques, mais bon...
et comme je suis nul en calcul j'avais aussi f(x) = ax qui est faux.
Sinon, je n'ai pas l'habitude de résoudre ces trucs là.
Alors je commencerai doucement,
en prenant quelques valeurs comme
x=0
f(0) = f(y)x f(0)
pour tout y, de là à penser que f(0) = 0 !
alors
pour y = 0
f(xf(x)) = x² je sais pas si c'est utile
avec x=1
f(f(y+1)) = f(y)f(1) +1
...
jamais bossé ces techniques, mais bon...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
juste quelques lignes car je fais erreur de calculs sur erreur de calculs.
je n'y connais rien aux méthodes de résolution de ces trucs là.
Mais il me semble que f(x) =-x marche aussi.
Ensuite en prenant des valeurs de 0 ou 1 pour x et y,
on obtient quelques renseignements:
x=0 va donner f(o) =0
y = 0 donne f(xf(x)) = x²
x=1
f(f(y+1) = f(yf(1)) +1
avec y=1
f(f(2)) = f(f(1)) + 1 = 2
f(f(y+1))= f(y) + 1
.................
bon doit y avoir des techniques de ce genre, ou mieux, j'imagine bien connues...
je n'y connais rien aux méthodes de résolution de ces trucs là.
Mais il me semble que f(x) =-x marche aussi.
Ensuite en prenant des valeurs de 0 ou 1 pour x et y,
on obtient quelques renseignements:
x=0 va donner f(o) =0
y = 0 donne f(xf(x)) = x²
x=1
f(f(y+1) = f(yf(1)) +1
avec y=1
f(f(2)) = f(f(1)) + 1 = 2
f(f(y+1))= f(y) + 1
.................
bon doit y avoir des techniques de ce genre, ou mieux, j'imagine bien connues...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
beagle a écrit:x=1
f(f(y+1) = f(yf(1)) +1
avec y=1
f(f(2)) = f(f(1)) + 1 = 2
f(f(y+1))= f(y) + 1
.................
bon doit y avoir des techniques de ce genre, ou mieux, j'imagine bien connues...
Juste par curiosité, comment tu trouves ta dernière ligne?
« Je ne suis pas un numéro, je suis un homme libre ! »
Monsieur23 a écrit:Juste par curiosité, comment tu trouves ta dernière ligne?
Euh, en truandant j'ai l'impression.
Zut encore de l'inversion dans les formules.
Bon, cet exo n'est à la base pas pour moi,
mais comme LeJeu a peur le soir tout seul sur les fils désertés,
il m'a lancé un pas malin :"beagle à toi!"
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Hello,
je proposerais, en considérant les solutions parmi les fonctions dérivables :
on a comme déjà dit=0, f(xf(x))=x^2) mais aussi
mais aussi )=-x^2 = -f(xf(x))) en appliquant la relation à y = -x. Donc si on considère l'ensemble I des images de xf(x) pour x réel, qui est comme f est supposée dérivable et à fortiori continue au moins un intervalle sinon tout R (TVI). Bref sur I f est donc impaire, et de fait f' est paire sur cet intervalle, ce qui est important pour la suite.
en appliquant la relation à y = -x. Donc si on considère l'ensemble I des images de xf(x) pour x réel, qui est comme f est supposée dérivable et à fortiori continue au moins un intervalle sinon tout R (TVI). Bref sur I f est donc impaire, et de fait f' est paire sur cet intervalle, ce qui est important pour la suite.
A présent, je dérive la relation par rapport à y, ce qui donne :
f'(xf(x+y))=f(x)f'(yf(x)))
En appliquant cette relation en y=0, on trouve :
(1) :f'(xf(x))=f(x)f'(0))
En l'appliquant pour y=-x, on trouve cette fois-ci:
f'(xf(0))=f(x)f'(-xf(x)))
c'est à dire en remplaçant f(0)=0
(2) :^2=f(x)f'(-xf(x)))
C'est ici qu'entre l'argument de parité de f' sur I, qui permet donc de dire que)=f'(xf(x))) , que l'on peut remplacer dans (2) au moyen de ce qu'on a obtenu par (1). Cela donne :
, que l'on peut remplacer dans (2) au moyen de ce qu'on a obtenu par (1). Cela donne :
^2=f(x)\frac{f(x)f'(0)}{xf'(x)}) , ce qui se simplifie en :
, ce qui se simplifie en :
}{f^2(x)}=\frac{1}{x^2f'(0)})
A présent ça tombe tout seul, en intégrant on a :
}=\frac{1}{xf'(0)}+C)
=\frac{xf'(0)}{1+Cxf'(0)})
Evidemment en redérivant f et en prenant en x=0 (pour retrouver f'(0)) on voit que la seule constante possible est C=0, donc on retombe sur f de la forme:
=xf'(0))
Donc si f est solution, elle est nécessairement de la forme f(x) = ax.
En remplaçant dans la relation initiale, on trouve = a^2yx+x^2) donc
donc 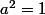
et on retombe sur les deux solutions déjà exhibées f(x)=x et f(x)=-x qui sont donc les seules solutions dérivables.
Modulo quelques points de rigueurs oubliés dans ma démo comme le traitement de la singularité en x=0 dans mes divisions au cours des calculs je pense que ça se tient :we:
Damien
je proposerais, en considérant les solutions parmi les fonctions dérivables :
on a comme déjà dit
A présent, je dérive la relation par rapport à y, ce qui donne :
En appliquant cette relation en y=0, on trouve :
(1) :
En l'appliquant pour y=-x, on trouve cette fois-ci:
c'est à dire en remplaçant f(0)=0
(2) :
C'est ici qu'entre l'argument de parité de f' sur I, qui permet donc de dire que
A présent ça tombe tout seul, en intégrant on a :
Evidemment en redérivant f et en prenant en x=0 (pour retrouver f'(0)) on voit que la seule constante possible est C=0, donc on retombe sur f de la forme:
Donc si f est solution, elle est nécessairement de la forme f(x) = ax.
En remplaçant dans la relation initiale, on trouve
et on retombe sur les deux solutions déjà exhibées f(x)=x et f(x)=-x qui sont donc les seules solutions dérivables.
Modulo quelques points de rigueurs oubliés dans ma démo comme le traitement de la singularité en x=0 dans mes divisions au cours des calculs je pense que ça se tient :we:
Damien
Ce fût sympatique 
Préliminaire: j'ai utilisé la transformation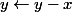 pour obtenir l'équation
pour obtenir l'équation
)=f((y-x)f(x))+x^2) ,
,
qui est un peu plus pratique pour travailler.
Donc:
- donne
donne =f(yf(0))) ..Si
..Si ) est non nul, ça implique
est non nul, ça implique  constante, mais
constante, mais  constante ne vérifie pas l'equation. Donc
constante ne vérifie pas l'equation. Donc =0) .
.
- donne
donne )=x^2) . En particulier, on obtient
. En particulier, on obtient =0) =>
=>
-Main tricks: est injective! Si
est injective! Si =f(y)) , le terme de gauche de l'équation devient
, le terme de gauche de l'équation devient )=f(xf(x))=x^2) ,
,
donc l'équation se simplifie enf(x))) . Par le point précédent, ça implique
. Par le point précédent, ça implique f(x)=0) . Si
. Si =0) (
() ), on sait déjá que
), on sait déjá que 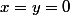 , sinon, on simplifie et
, sinon, on simplifie et 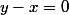 .
.
- est impaire:
est impaire: )=f(xf(x))=x^2) , donc par injectivité
, donc par injectivité =xf(x)) et on simplifie par
et on simplifie par  (si
(si  non nul) pour obtenir l'imparité.
non nul) pour obtenir l'imparité.
En particulier, est solution de l'equation si et seulement si
est solution de l'equation si et seulement si 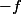 l'est.
l'est.
-Calcul de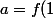) : L equation
: L equation )=x^2) devient pour
devient pour  :
: =1) . Puis pour
. Puis pour  :
:  , donc
, donc 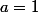 ou
ou 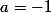 .. Quitte á remplacer
.. Quitte á remplacer  par
par 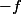 , on peut supposer dorénavant que
, on peut supposer dorénavant que =1) .
.
-On reprend l'équation: pour ,
, =f(y-1)+1)
pour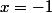 , et en utilisant l'imparité,
, et en utilisant l'imparité, =f(y+1)-1)
Les deux équations ensemble impliquent la relation=f(t)+2) ..En particulier,
..En particulier, =2)
-Pour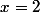 , l'équation devient
, l'équation devient )=f(2y-4)+4)
En utilisant le fait que=f(t)+2) , ça devient
, ça devient )=f(2y))
En utilisant l'injectivité, ça devient=2y)
Donc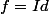 (ou
(ou 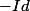 quand
quand =-1) )..ouf :we:
)..ouf :we:
Préliminaire: j'ai utilisé la transformation
qui est un peu plus pratique pour travailler.
Donc:
-
-
-Main tricks:
donc l'équation se simplifie en
-
En particulier,
-Calcul de
-On reprend l'équation: pour
pour
Les deux équations ensemble impliquent la relation
-Pour
En utilisant le fait que
En utilisant l'injectivité, ça devient
Donc
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
