Equation fonctionelle
36 messages
- Page 2 sur 2 - 1, 2
Pour le moment, j'ai (dans cet ordre) :
f(1)=a
f(2)=2a²
f(5)=4a^4+a²
f(8)=8a^4
f(7)²=32a^8+16a^6+2a^4-a² (car 7²+1²=5²+5²)
f(4)²=32a^8-16a^6-2a^4+2a² (car 4²+7²=8²+1²)
Aprés je suis un peu sec... je me demande s'il faut chercher d'autres f(?) ou bien regarder les 2 dernières comme des équations diophantiennes et essayer de les "résoudre"...
f(1)=a
f(2)=2a²
f(5)=4a^4+a²
f(8)=8a^4
f(7)²=32a^8+16a^6+2a^4-a² (car 7²+1²=5²+5²)
f(4)²=32a^8-16a^6-2a^4+2a² (car 4²+7²=8²+1²)
Aprés je suis un peu sec... je me demande s'il faut chercher d'autres f(?) ou bien regarder les 2 dernières comme des équations diophantiennes et essayer de les "résoudre"...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bon, je complète mon post précédent (mais c'est quand même à peine bourin)
=a\ \ f(2)=2a^2\ \ f(5)=4a^4+a^2\ \ f(8)=8a^4\ \ f(7)^2=32a^8+16a^6+2a^4-a^2) (car 7²+1²=5²+5²)
(car 7²+1²=5²+5²) ^2=32a^8-16a^6-2a^4+2a^2) (car 4²+7²=8²+1²)
(car 4²+7²=8²+1²)
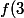=b\ \ \ f(10)=a^2+b^2\ \ \ f(11)^2=16a^8+8a^6-2a^4+2a^2b^2+b^4) (car 11²+2²=10²+5²)
(car 11²+2²=10²+5²) =4a^4+b^2\) mais aussi
mais aussi ^2=48a^8+24a^6-2a^2+2a^2b^2+b^4) (car 13²+2²=11²+7²)
(car 13²+2²=11²+7²)
On en tire (en utilisant le fait que a est non nul) que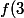=b=2a^2+1\ \ f(10)=4a^4+5a^2+1\ \ f(11)^2=32a^8+48a^6+30a^4+10a^2+1) (car 11²+2²=10²+5²)
(car 11²+2²=10²+5²) ^2=32a^6+32a^4+15a^2+2) (car 9²+7²=11²+3²)
(car 9²+7²=11²+3²) ^2=-32a^8+16a^6+34a^4+16a^2+2) (car 6²+7²=9²+2²)
(car 6²+7²=9²+2²)
La seule façon d'avoir f(6)² carré parfait (donc positif) est de prendre a=1
d'où f(n)=n pour tout n de 1 à 10 et donc f(n)=n pour tout entier n
(ouf!!!)
On en tire (en utilisant le fait que a est non nul) que
La seule façon d'avoir f(6)² carré parfait (donc positif) est de prendre a=1
d'où f(n)=n pour tout n de 1 à 10 et donc f(n)=n pour tout entier n
(ouf!!!)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Salut,
Clairement,=f(n)^2)
Donc = 1) comme
comme  est définie sur
est définie sur 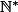 . On en déduit
. On en déduit  = (f^1^2 + 1^2) = 2f(1)^2 = 2) . On montre de même
. On montre de même  = 4) ,
,  = 5) et
et  = f(3)^2 + f(4)^2 = f(3)^2 + 16) , d'où
, d'où 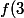^2 = 9) , i.e,
, i.e, 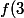 = 3) .
.
Bref, il semble que = n) soit solution.
soit solution.
On considère le lemme suivant :\in\mathbb{N}^3 \,:\, n^2 = a^2 + b^2 - c^2)
Preuve :^2 = (4n - k)^2 + (2n + 2k)^2 - (2n-2k)^2)
Lorsque vaut 0,1,2 ou 3,
vaut 0,1,2 ou 3, 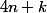 parcourt
parcourt  et les entiers considérés sont bien naturels, d'où le résultat.
et les entiers considérés sont bien naturels, d'où le résultat.
Par récurrence forte, supposons = k) pour tout
pour tout 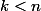 . Le lemme se réécrit
. Le lemme se réécrit 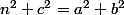 et on a :
et on a :
^2 = f(a)^2 + f(b)^2 - f(c)^2 = a^2 + b^2 - c^2 = n^2)
D'où = n) .
.
Clairement,
Donc
Bref, il semble que
On considère le lemme suivant :
Preuve :
Lorsque
Par récurrence forte, supposons
D'où
Si on regarde la relation dont tu te sert pour la récurrence, c'est une de celles que je proposait dans le post #1 (avec des valeurs de g,h,k,k' différentes de celles que j'ai pris) et la réccurence marche évidement avec n'importe quelle relation de ce type (en prenant une matrice de O(2) diffférente, tu peut trouver des tas d'autres relations)
Et, en ce qui concerne les "cas particuliers", le fait que f(0) n'existe pas 'corse' trés nettement le problème...
Si tu as une solution plus simple que celle du post #27, je suis preneur...
P.S.1 : "ne pas la définir en 0 ne sert à rien" : je ne suis pas du tout d'accord, cela sert à... rendre le problème nettement plus complexe.
P.S.2 : dans ton lemme, pour faire une récurrence, il faudrait en plus que a,b et c soient >0 et
Et, en ce qui concerne les "cas particuliers", le fait que f(0) n'existe pas 'corse' trés nettement le problème...
Si tu as une solution plus simple que celle du post #27, je suis preneur...
P.S.1 : "ne pas la définir en 0 ne sert à rien" : je ne suis pas du tout d'accord, cela sert à... rendre le problème nettement plus complexe.
P.S.2 : dans ton lemme, pour faire une récurrence, il faudrait en plus que a,b et c soient >0 et
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
36 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

 ) on a
) on a