Equation fonctionelle
Olympiades mathématiques, énigmes et défis
-
kasmath
- Membre Relatif
- Messages: 186
- Enregistré le: 24 Mai 2009, 22:38
-
 par kasmath » 20 Juin 2010, 21:02
par kasmath » 20 Juin 2010, 21:02
trouvez tous les fonction
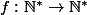
tel que :
)=f(m)^2+n,\forall m,n \in \mathbb{N}^*.)
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 20 Juin 2010, 21:38
par windows7 » 20 Juin 2010, 21:38
on a
f(n) <= n
donc f(1)=1
f(2) = f( 1 + f(1) ) = f(1)² +1 = 2
f(3) =f( 1 + f(2) ) = f(1)²+3 = 3
patati patata

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 21 Juin 2010, 10:20
par Ben314 » 21 Juin 2010, 10:20
windows7 a écrit:... f(n) <= n ...
Et pourqoui donc ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 21 Juin 2010, 10:45
par windows7 » 21 Juin 2010, 10:45
salut ben
parce que dans IR on a deja pas bien le choix ..
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 21 Juin 2010, 11:06
par Doraki » 21 Juin 2010, 11:06
c'est pas parcequ'on a une fonction de N* dans N* qui vérifie ces équations qu'on a une fonction de R dans R qui étend la fonction de départ tout en continuant à vérifier les équations pour n et m non-entiers.
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 21 Juin 2010, 11:16
par windows7 » 21 Juin 2010, 11:16
oui oui oui oui oui mais on voit mieu les choses dans IR
suffit de remarquer de fof est affine en realité
-
kasmath
- Membre Relatif
- Messages: 186
- Enregistré le: 24 Mai 2009, 22:38
-
 par kasmath » 21 Juin 2010, 11:25
par kasmath » 21 Juin 2010, 11:25
windows7 a écrit:on a
f(n) <= n
donc f(1)=1
f(2) = f( 1 + f(1) ) = f(1)² +1 = 2
f(3) =f( 1 + f(2) ) = f(1)²+3 = 3
patati patata
tu pourrais pas poser quq chose sans démontrer

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 21 Juin 2010, 11:25
par Ben314 » 21 Juin 2010, 11:25
1) Pour tout
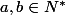
, si
=f(b))
alors
^2+a\,=\,f\big(1^2+f(a)\big)\,=\,f\big(1^2+f(b)\big)\,=\,f(1)^2+b)
donc

: f est injective.
2) Pour tout
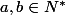
, on a :
^2+1\big]\,<br />=\,f\big[a^2+f\big(f(b)^2+f(1)\big)\big]\,<br />=\,f(a)^2+f(b)^2+f(1)\,<br />=\,f\big[b^2+f\circ f(a)^2+1\big])
(par symétrie)
donc
^2+1=b^2+f\circ f(a)^2+1)
(injectivité) ce qui montre que
^2-n^2)
est constante.
Si on note

cette constante, alors, pour tout
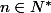
,
^2=n^2+K)
doit être un carré et cela n'est possible que si
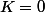
.
On en déduit que, pour tout
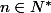
,
^2=n^2)
, c'est à dire que
=n)
.
3) Pour tout
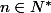
, on a
\,=\,f\big(1^2+f\circ f(n)\big)=f(1)^2+f(n)=f(n)+a^2)
si on pose
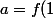)
.
On en déduit (récurrence) que
=a+(n-1)a^2=a^2n-a^2+a)
.
Or, on doit avoir
\big)=f(1)^2+n)
, c'est à dire
-a^2+a=a^2+n)
ce qui n'est possible que si
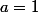
Conclusion : Pour tout
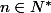
,
=n)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
kasmath
- Membre Relatif
- Messages: 186
- Enregistré le: 24 Mai 2009, 22:38
-
 par kasmath » 21 Juin 2010, 11:33
par kasmath » 21 Juin 2010, 11:33
Ben314 a écrit:1) Pour tout
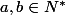
, si
=f(b))
alors
^2+a\,=\,f\big(1^2+f(a)\big)\,=\,f\big(1^2+f(b)\big)\,=\,f(1)^2+b)
donc

: f est injective.
2) Pour tout
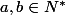
, on a :
^2+1\big]\,<br />=\,f\big[a^2+f\big(f(b)^2+f(1)\big)\big]\,<br />=\,f(a)^2+f(b)^2+f(1)\,<br />=\,f\big[b^2+f\circ f(a)^2+1\big])
(par symétrie)
donc
^2+1=b^2+f\circ f(a)^2+1)
(injectivité) ce qui montre que
^2-n^2)
est constante.
Si on note

cette constante, alors, pour tout
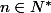
,
^2=n^2+K)
doit être un carré et cela n'est possible que si
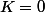
.
On en déduit que, pour tout
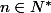
,
^2=n^2)
, c'est à dire que
=n)
.
3) Pour tout
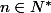
, on a
\,=\,f\big(1^2+f\circ f(n)\big)=f(1)^2+f(n)=f(n)+a^2)
si on pose
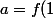)
.
On en déduit (récurrence) que
=a+(n-1)a^2=a^2n-a^2+a)
.
Or, on doit avoir
\big)=f(1)^2+n)
, c'est à dire
-a^2+a=a^2+n)
ce qui n'est possible que si
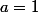
Conclusion : Pour tout
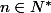
,
=n)
presque comme mon idée
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 21 Juin 2010, 12:10
par windows7 » 21 Juin 2010, 12:10
propose un truc compliqué et on verra mais bon la ..
dailleurs cest bcp plus general que cela
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 21 Juin 2010, 12:13
par windows7 » 21 Juin 2010, 12:13
je suis pas sur d'avoir bien lu
n²+k est un carré => k=0 ?
pythagore et ces fameux triplets sont plus d'actualité ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 21 Juin 2010, 12:24
par Nightmare » 21 Juin 2010, 12:24
n² + k doit être un carré pour tout n ! En particulier, pour n=2 ...
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 21 Juin 2010, 12:32
par windows7 » 21 Juin 2010, 12:32
oui et ya combien de K verifiants ca ? je vois bcp !
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 21 Juin 2010, 12:46
par Doraki » 21 Juin 2010, 12:46
Si k > 0 et n > (k-1)/2, alors n²+k ne peut pas être un carré.
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 21 Juin 2010, 13:04
par windows7 » 21 Juin 2010, 13:04
oui oui j'avoue jveux casser les burnes un peu :D
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 21 Juin 2010, 14:00
par windows7 » 21 Juin 2010, 14:00
bon je donne quand meme ma reponse ..
fof=id
on montre f croissante de la facon suivante
comme fof=id alors n=f(k)
donc f(m²+f(n)) = f(m²+k) = f(m)²+f(k)
on prend m=1 on a alors
f(1+k)=f(1)²+f(k)
donc f(1+k)-f(k) > 0 f croissante
montrons juste f(n)=n
si f(n) > n
=> fof(n) > f(n) par croissance
fonc n > f(n)
donc f(n)=n
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 21 Juin 2010, 14:02
par windows7 » 21 Juin 2010, 14:02
windows7 a écrit:bon je donne quand meme ma reponse ..
fof=id
on montre f croissante de la facon suivante
comme fof=id alors n=f(k)
donc f(m²+f(n)) = f(m²+k) = f(m)²+f(k)
on prend m=1 on a alors
f(1+k)=f(1)²+f(k)
donc f(1+k)-f(k) > 0 f croissante
montrons juste f(n)=n
si f(n) > n
=> fof(n) > f(n) par croissance
fonc n > f(n)
donc f(n)=n
idem si f(n) < n

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 21 Juin 2010, 16:30
par Ben314 » 21 Juin 2010, 16:30
windows7 a écrit:...fof=id...
Pourqoui ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 21 Juin 2010, 17:06
par windows7 » 21 Juin 2010, 17:06
comme je l'ai di je ne c plus quand c'est bien plus general que juste le cas exposé par notre ami.
tu veux une autre demo que la tienne pour fof = id ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
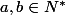 , si
, si =f(b)) alors
alors ^2+a\,=\,f\big(1^2+f(a)\big)\,=\,f\big(1^2+f(b)\big)\,=\,f(1)^2+b) donc
donc  : f est injective.
: f est injective.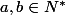 , on a :
, on a :^2+1\big]\,<br />=\,f\big[a^2+f\big(f(b)^2+f(1)\big)\big]\,<br />=\,f(a)^2+f(b)^2+f(1)\,<br />=\,f\big[b^2+f\circ f(a)^2+1\big]) (par symétrie)
(par symétrie)^2+1=b^2+f\circ f(a)^2+1) (injectivité) ce qui montre que
(injectivité) ce qui montre que ^2-n^2) est constante.
est constante. cette constante, alors, pour tout
cette constante, alors, pour tout 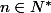 ,
, ^2=n^2+K) doit être un carré et cela n'est possible que si
doit être un carré et cela n'est possible que si 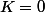 .
.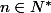 ,
, ^2=n^2) , c'est à dire que
, c'est à dire que =n) .
.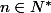 , on a
, on a \,=\,f\big(1^2+f\circ f(n)\big)=f(1)^2+f(n)=f(n)+a^2) si on pose
si on pose 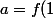) .
.=a+(n-1)a^2=a^2n-a^2+a) .
.\big)=f(1)^2+n) , c'est à dire
, c'est à dire -a^2+a=a^2+n) ce qui n'est possible que si
ce qui n'est possible que si 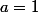
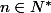 ,
, =n)
, si
alors
donc
: f est injective.
, on a :
(par symétrie)
(injectivité) ce qui montre que
est constante.
cette constante, alors, pour tout
,
doit être un carré et cela n'est possible que si
.
,
, c'est à dire que
.
, on a
si on pose
.
.
, c'est à dire
ce qui n'est possible que si
,
