Tu procède soit comme Imod le dit en prenant pour un
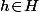
donné une expression de

en fonction des
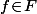
qui soit de longueur minimale, soit par récurrence sur la longueur des mots.
Au niveau des calculs, ça revient très très exactement au même, mais contrairement à Imod, j'aurais tendance à préférer la récurrence (parce que ça évite de faire de l'absurde et que ça donne vaguement l'impression qu'on a un algorithme de réduction)
On considère donc le proposition
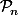
:
Tout 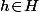 pouvant s'écrire
pouvant s'écrire 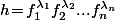 avec
avec 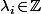 ,
, 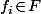 peut aussi s'écrire
peut aussi s'écrire 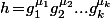 avec
avec 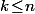 et où les
et où les 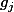 sont des éléments distincts de
sont des éléments distincts de 
(et
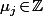
).
L'amorce pour

(et

) est évidente.
Pour l'hérédité, on suppose que la propriété est vrai pour un certain

et on considère
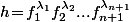
.
Vu l'hypothèse de récurrence, on peut se ramener à un cas où
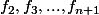
sont distincts.
Si

est distinct des
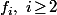
, c'est fini.
Si

est égal à un certain
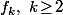
alors vu l'hypothèse faite sur

(plus une mini récurrence), on sait que
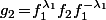
est dans

.
On a alors
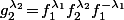
c'est à dire
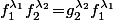
.
De même,
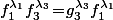
pour un certain
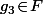
,
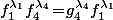
, etc...
On a donc
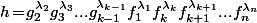
Or, comme
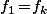
on a
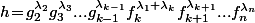
qui est une écriture de

ne contenant plus que

éléments (sans doute non distincts) de

et grâce à l'hypothèse de récurrence, cela montre qu'il y a une écriture de

ne contenant que des éléments distincts de

.
En fait, cette partie "calculs", on peut aussi "l'enrober" en disant que, lorsqu'une écriture de

contient au moins un "doublon", alors on peut "simplifier" ce doublon et que, bien que ça risque de provoquer l'apparition de nouveaux "doublons" (à mon avis c'était ça ton problème)
comme ça a fait diminuer de 1 la "pseudo-longueur" (*) du mot en question, ça signifie qu'on ne pourra pas continuer ad vitam aeternam à simplifier des doublons.
C'est pour ça que ce que proposait Imod est éventuellement plus simple au niveau raisonnement (mais c'est évidement les mêmes calculs) : si au départ tu suppose que tu as une écriture de
longueur minimale de

et que tu suppose qu'elle contient un doublon tu arrive à la conclusion qu'on pouvait diminuer la longueur ce qui est absurde.
(*) Dans la littérature, ce qu'on appelle en général la "longueur" du mot, ça serait plutôt la somme des valeurs absolue des

, sauf que cette "longueur" là, elle risque de na pas diminuer.
P.S. C'est éventuellement moins chiant à rédiger dans le cas particulier où

désigne l'ensemble des éléments d'ordre fini de

vu que

est non seulement "stable par conjugaison", mais il est aussi "stable par puissances" : si
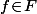
alors
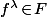
pour tout
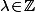
donc dans la preuve, on peut se passer des exposants.


 mais sans doute sur une mauvaise piste...
mais sans doute sur une mauvaise piste...