Sur le groupe des homéomorphismes croissants de R

[mathelot]

un autre

[Ben314]

Là t'as un monoide distingué, mais pas un groupe.

Effectivement (ça m'apprendra à essayer de faire 36.000 choses à la fois...)

Effectivement, on peut dire que c'est le lemme fondamental pour étudier la structure de groupe des homéos de R, qu'on peut résumer ainsi :
Si (f(x)>x g(x)>x ), alors f et g sont conjugués dans G.

Effectivement (aussi), c'est un "bon résumé" mais il faut rajouter dans l'hypothèse " Si (f(x)>x g(x)>x ) ET (f(x) g(x)x} et Bf={x/f(x)<x}, alors f et g sont conjuguées ssi (Af,Bf) "est de même nature topologique" que (Ag,Bg), i.e. il existe un h de G tel que h(Af)=Ag et h(Bf)=Bg.

[ffpower]

Exact, j'avais un peu trop résumé^^
Et en effet c'est pas si compliqué que ça à démontrer..

[mathelot]

re,

question sur le B-A-BA de théorie des groupes:

quel est le lien entre les deux sous-groupes propres et distingués que j'ai exhibés (le 1er a été validé par ffpower, le second était faux tandis le 3ème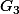 "marche")

et les classes de conjugaison ?


D'après Ben314, les classes de conjugaison correspondent aux propriétés topologiques des deux ouverts A={x / f(x)-x>0} et B={x / f(x)-x<0}

ça fait beaucoup de classes , étant que A (resp B) peuvent être compacts ou non,connexes on non, avec des cardinalités de composantes
connexes finies, dénombrables, non dénombrables,etc..

Pourquoi on trouve au moins deux sous-groupes ?

je ne fais pas le lien, en théorie des groupes, entre classes de conjugaison
et sous-groupes distingués.

[Doraki]

un sous-groupe distingué est une réunion de classes de conjugaisons qui forme un groupe.

G3 n'est pas distingué parcequ'il ne contient pas la fonction x -> e*((x/e)+1) = x+e, conjuguée de x -> x+1.

Deux fonctions f1 et f2 sont conjugués <=> il existe g dans G tel que f1°g = g°f2.
On peut être un peu plus précis et dire que si on appelle f'(x) = signe de f(x)-x,
f1 et f2 sont conjuguées <=> il existe g dans G tel que f1' ° g = f2'
Les classes de conjugaison sont donc les fonctions continues de R dans {-,0,+} (où les ouverts sont {},{-},{+},{-,0,+}) quotienté par l'action des homéomorphismes croissants de R.

Pour f dans G, j'appelle l'ouvert {x / f(x) <> x} le support de f.

Les 3 sous-groupe distingués sont G1 = {f / support de f est borné},
qui est l'intersection de G2 = {f / support de f est minoré} et de G3 = {f / support de f est majoré}

[Ben314]

re,
quel est le lien entre les deux sous-groupes propres et distingués que j'ai exhibés (le 1er a été validé par ffpower, le second était faux tandis le 3ème "marche")

et les classes de conjugaison ?
ça fait beaucoup de classes , étant que A (resp B) peuvent être compacts ou non,connexes on non, avec des cardinalités de composantes
connexes finies, dénombrables, non dénombrables,etc..

Non, ton ensemble G3 n'est pas distingué : si on conjugue la fonction f:x->x+1 (qui est dans G3) par h:x->racine(2).x (qui est dans G) on obtient x->x+racine(2) (qui n'est pas dans G3).

Pour les classes, je confirme (à tête reposé) qu'elles sont entièrement définies par "les propriétés topologiques" de la partition (Af,R\(AfuBf),Bf) associée à la fonction f et donc qu'il y a effectivement "beaucoup de classes" (au moins la puissance du continu).

Aprés, le lien en classes de conjugaisons et sous groupe distingué, ben c'est que (par définition), un sous groupe H est distingué ssi il est réunion de classes de conjugaison (i.e. dés qu'il contient une fonction f, il doit contenir tout les conjugués de f).

Ensuite, dans un "trés gros" groupe comme celui là qui est "extrèmement" non commutatif, on sent bien que la classe de conjugaison d'un élément va être "trés grosse" et donc que dans la recherche des sous groupes distingués, c'est plutôt le mot "distingué" qui est le plus "restrictif".

EDIT : Grilled...

[ffpower]

Deux fonctions f1 et f2 sont conjugués il existe g dans G tel que f°g = g°f.
On peut être un peu plus précis et dire que si on appelle f'(x) = signe de f(x)-x,
f1 et f2 sont conjuguées il existe g dans G tel que f' ° g = g'

Quelques coquilles de notations là dedans, tu devrais remettre ça dans l'ordre :we:

Pour les classes, je confirme (à tête reposé) qu'elles sont entièrement définies par "les propriétés topologiques" de la partition (Af,R\(AfuBf),Bf) associée à la fonction f et donc qu'il y a effectivement "beaucoup de classes" (au moins la puissance du continu).

En fait, exactement la puissance du continu, puisque G tout entier a la puissance du continu.


Je vais tenter de résumer la situation actuelle :
Donc je commence par rappeller que u et v sont conjugués s'il existe g dans G tel que v o g=g o u. Cette relation montre que les oscillations de u autour de Id et de v autour de Id sont fortement liées, et en fait on peut montrer que ces oscillations sont la seule chose importante pour être conjugués dans G. C'est ce qui a été exprimé de différentes manieres par moi, Ben et Doraki. A titre d'exemple, les homéos x->x^3 et x->x^5 sont conjugués, ce qui est a priori pas trivial.

Donc expliquons vite fait pourquoi si par exemple u>Id et v>Id, alors u et v sont conjugués. On veut construire un homeo g tel que pour tout x, v(g(x))=g(u(x)). L'idée est que si on a défini g en un certain x, alors la relation précédente impose ce que vaut g en u(x), et donc ensuite en u o u(x), ect.. On va donc définir g un peu au hasard sur un intervalle bien choisi, puis de prolonger g de proche en proche grace à cette relation. Plus rigoureusement: Soit I0=[0,u(0)[ et J0= [0,v(0)[, et g un homéo croissant de I0 sur J0 quelconque, disons affine par exemple. On va prolonger g en un homéo de R vérifiant la relation que l'on souhaite. Pour k entier relatif, soit Ik=u^k(I0) et Jk=v^k(J0). On vérifie que les Ik, k dans Z, forment une partition de R, idem pour les Jk. Un élément de Ik est de la forme u^k(x) avec x dans I0, ce qui permet de définir g:Ik->Jk par g(u^k(x))=v^k(g(x)). On ainsi définit g sur R tout entier et on vérifie aisément que c'est bien un homéo croissant et que g o u=v o g

Dans le cas général où u-Id et v-Id sont toujours de même signe ( en considérant 0 comme un signe à part ), on peut là encore conjugué u et v, on peut là encore construire une conjugaison g de u sur v, en effectuant une construction de g comme précédemment sur chaque intervalle dont sont composés les ouverts Au={u>Id} et Bu={uId, alors si v est un homéo quelconque de G "suffisamment" proche de Id, alors u o v>Id donc u o v et u sont conjugués, donc u o v est dans H, et donc v est dans H. Et comme tout élémént de G est conjugué à un élément proche de Id, on obtient que H=G. Avec ce genre d'idée, on peut montrer que les seuls sous groupes distingués de G sont {Id},G et les 3 sous groupes spéciaux G1, G2 et G3 dont a parlé Doraki.

Reste donc maintenant la question des automorphismes de G. Comme l'a souligné Doraki, il en existe des non interieurs, à savoir les u->vuv^{-1}, ou v est un homéo décroissant de R, et comme l'a supputé Ben, ce sont les seuls, mais ceci reste encore à prouver. Le "lemme de conjugaison" sera bien sur encore de la partie, mais bon, va falloir aussi dire d'autres trucs^^

[ffpower]

Le sujet coule dangereusement ( 4eme topic..vive cette nouvelle section XD ) donc petit up vu qu'il reste toujours la question 2 à torcher.. Comme pour la question 1, je demande pas de détails rébarbatifs, juste les idées. Donc déjà la question à se poser pour démarrer : Si T est un automorphisme de G, et supposons que l'on sache que T est de la forme u->vuv^{-1}, comment récupérer v à partir de T?

[Doraki]

Si on montre que les sous-groupe maximaux de G sont les groupes de la forme Ga = {f / f(a)=a},

alors pour tout a il existe b tel que T(Ga) = Gb,
On prend alors v(a) = b.
C'est une bijection, et il resterait à montrer que c'est un homéomorphisme.

[ffpower]

Ceci est faux, car ton sous groupe G1 des fonctions "à support fini" n'est inclu dans aucun de tes Ga. Apres on pourrait rectifier l'énoncé en " tout sous groupe maximal ne contenant pas G1 est un Ga", ce qui serait suffisant. Et effectivement cette idée pourrait alors être interessante. Mais même là, je ne suis pas sur que ce soit vrai. Ce que je veux dire, c'est que le fait de pouvoir conjuguer les fonctions donnait beaucoup de souplesse pour l'étude des sous groupes distingués, mais maintenant qu'on laisse de coté la partie "distinguée", la structure des sous groupes devient probablement ultra chaotique, et je me demande si il n'y aurait pas des sous groupes vraiment monstrueux, même parmi les sous groupes maximaux..Enfin c'est du purement spéculatif, rien de sur, après tout c'est possible aussi que tout sous groupe max "moche" contient G1^^

[Doraki]

Peut-être qu'il n'y a pas de sous-groupe maximal contenant G1.
Ou alors on pourrait parler des sous-groupe maximaux de G1 (vu que T laisse G1 globalement invariant, on y perd rien)
(chuis d'accord que de toutes façons on est mal barré pour prouver qu'un sous-groupe maximal doit être d'une certaine forme)

[ffpower]

Peut-être qu'il n'y a pas de sous-groupe maximal contenant G1.

Ouais, remarque..Je me disais qu'il y en avait forcément par Zorn, mais en fait non. Du coup ca me redonne de l'espoir sur le fait que ta méthode puisse aboutir