Bonjour
Voici de nouveau un gâteau d'anniversaire avec 7 bougies à éteindre. Mais la règle a changé:
Les yeux bandés, le (ou la) gamin(e) souffle sur une bougie au hasard mais malheureusement
si la bougie est éteinte elle va s'allumer de nouveau.
La famille et les amis ne pourront boire le champagne que si les 7 bougies sont éteintes.
En moyenne l'enfant met 5 secondes pour souffler sur une bougie.
Combien de temps va-t-on attendre pour boire le champagne?
7 bougies à souffler de façon aléatoire.
8 messages
- Page 1 sur 1
Re: 7 bougies à souffler de façon aléatoire.
Salut,
Sauf erreur, il faut en moyenne 2416/15 étapes de 5 secondes (soit environ 161.066 étapes) pour que toutes les bougies soient éteintes.
Sauf erreur, il faut en moyenne 2416/15 étapes de 5 secondes (soit environ 161.066 étapes) pour que toutes les bougies soient éteintes.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: 7 bougies à souffler de façon aléatoire.
Bonjour
Oui c'est bien cela.
Pour le calcul je suis parti de n=1 (c'est à dire 6 bougies allumées et 1 éteinte)
car c'est la seule possibilité à la première étape. Ensuite j'ai calculé "de 2 en 2" puisque la parité du nombre de bougies allumées change à chaque étape. Cela réduit la taille des calculs.
Oui c'est bien cela.
Pour le calcul je suis parti de n=1 (c'est à dire 6 bougies allumées et 1 éteinte)
car c'est la seule possibilité à la première étape. Ensuite j'ai calculé "de 2 en 2" puisque la parité du nombre de bougies allumées change à chaque étape. Cela réduit la taille des calculs.
Re: 7 bougies à souffler de façon aléatoire.
Salut
Lorsqu'on fait une simulation de par exemple 400000 expériences, on obtient effectivement une moyenne proche de 161 étapes, soit environ 13 min 25 s à souffler sur le gâteau. Gare aux bactéries !
Lorsqu'on fait une simulation de par exemple 400000 expériences, on obtient effectivement une moyenne proche de 161 étapes, soit environ 13 min 25 s à souffler sur le gâteau. Gare aux bactéries !
- Fichiers joints
-
- 7bougies.gif (53.35 Kio) Vu 676 fois
Re: 7 bougies à souffler de façon aléatoire.
Ce type de calcul d'espérance, c'est très courant dans les casse-têtes et perso., la façon dont je procède, j'aurais tendance à appeler ça "processus stochastique avec état de sortie" :
On note le vecteur colonne des probas des différents états non finaux après
le vecteur colonne des probas des différents états non finaux après  étapes et
étapes et  la matrice de transition de façon à avoir
la matrice de transition de façon à avoir 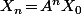 .
.
Donc ici, c'est un vecteur de
c'est un vecteur de  lignes (où
lignes (où 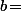 nombre de bougies) contenant les proba. qu'après
nombre de bougies) contenant les proba. qu'après  "soufflages" il y ait
"soufflages" il y ait 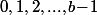 bougies éteintes ;
bougies éteintes ; 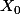 c'est le vecteur colonne (1 0 0 0 ...) et
c'est le vecteur colonne (1 0 0 0 ...) et  c'est la matrice
c'est la matrice 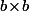 entièrement nulle sauf au dessus de la diagonale où on a
entièrement nulle sauf au dessus de la diagonale où on a 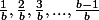 et en dessous de la diagonale où on a
et en dessous de la diagonale où on a 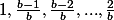 .
.
La proba. qu'après étapes le processus ne soit toujours pas fini c'est la somme des coordonnées de
étapes le processus ne soit toujours pas fini c'est la somme des coordonnées de  , c'est à dire
, c'est à dire 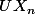 où
où  est le vecteur ligne
est le vecteur ligne ) donc la proba que le processus s'arrête en exactement
donc la proba que le processus s'arrête en exactement  étapes, c'est
étapes, c'est 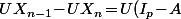A^{n-1}\!X_0) et l'espérance du temps d'arrêt, c'est :
et l'espérance du temps d'arrêt, c'est :
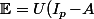\Big(\!\sum_{n\geq 1}\!nA^{n-1}\!\Big)X_0=U(I_p\!-\!A)\big(I_p\!-\!A\big)^{\!-2}\!X_0=U\big(I_p\!-\!A\big)^{-1}\!X_0=UY)
C'est à dire la somme des coordonnées du vecteur colonne solution du système
solution du système Y\!=\!X_0) et jusque là, ça s'applique à tout les problème de ce type où on cherche l'espérance du "temps de sortie" du processus.
et jusque là, ça s'applique à tout les problème de ce type où on cherche l'espérance du "temps de sortie" du processus.
Dans le cas présent, si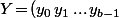) en colonne, le système
en colonne, le système Y\!=\!X_0) donne
donne
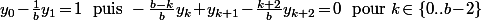 (avec
(avec 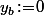 pour la dernière équation)
pour la dernière équation)
La somme des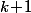 premières équation donne
premières équation donne 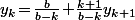 qui permet de calculer les
qui permet de calculer les 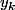 "en cascade" en partant de
"en cascade" en partant de 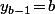 (j'ai pas cherché à regarder s'il y avait une "jolie" formule générale avec
(j'ai pas cherché à regarder s'il y avait une "jolie" formule générale avec  quelconque)
quelconque)
On note
Donc ici,
La proba. qu'après
C'est à dire la somme des coordonnées du vecteur colonne
Dans le cas présent, si
La somme des
Modifié en dernier par Ben314 le 02 Déc 2017, 19:18, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: 7 bougies à souffler de façon aléatoire.
En codant de sorte à souffler des gâteaux à p bougies, je me suis rendu compte d'un "résultat" (conjecture ?) que je ne connaissais pas : la suite qui associe au nombre de bougies à éteindre le nombre d'essais moyens à effectuer est semble t-il géométrique ( et serait de raison proche ou égale à 2).
J'en veux pour motivation de la conjecture le graphique suivant, en échelle logarithmique (sachant que j'ai eu des droites mieux dessinées que celle ici présente)
PS : je n'ai pas l'impression que le fichier joint soit passé. J'essaierai plus tard de le faire passer
Le fichier ne passant pas, voici la suite des rapports entre 2 termes consécutifs de la suite (sachant que la moyenne du nombre de souffles pour chaque p bougies est faite sur 100 essais)
[3.84,
2.776041666666667,
2.0938086303939962,
2.0940860215053765,
1.6872058194266153,
1.8906923662186153,
1.9067739771965126,
2.4127330284910307,
1.5910429483628303,
2.319711186043102,
1.4758101467823228,
2.482444823912939,
2.1928741471661337,
1.7651446839098826,
1.9710174881117386]
Le premier de 3.84 étant à exclure étant donné qu'il s'agit du passage de 1 bougies à 2 bougies. Je pense que je ne peux pas mettre de fichier à cause de mon manque d'ancienneté, mais visuellement en échelle log, ça fait une jolie droite !
J'en veux pour motivation de la conjecture le graphique suivant, en échelle logarithmique (sachant que j'ai eu des droites mieux dessinées que celle ici présente)
PS : je n'ai pas l'impression que le fichier joint soit passé. J'essaierai plus tard de le faire passer
Le fichier ne passant pas, voici la suite des rapports entre 2 termes consécutifs de la suite (sachant que la moyenne du nombre de souffles pour chaque p bougies est faite sur 100 essais)
[3.84,
2.776041666666667,
2.0938086303939962,
2.0940860215053765,
1.6872058194266153,
1.8906923662186153,
1.9067739771965126,
2.4127330284910307,
1.5910429483628303,
2.319711186043102,
1.4758101467823228,
2.482444823912939,
2.1928741471661337,
1.7651446839098826,
1.9710174881117386]
Le premier de 3.84 étant à exclure étant donné qu'il s'agit du passage de 1 bougies à 2 bougies. Je pense que je ne peux pas mettre de fichier à cause de mon manque d'ancienneté, mais visuellement en échelle log, ça fait une jolie droite !
Re: 7 bougies à souffler de façon aléatoire.
Si tu calcule les valeurs exactes des espérances, tu verra que ce n'est pas une suite géométrique : le rapport entre deux termes est de plus en plus proche de 2, mais pas égal à 2.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: 7 bougies à souffler de façon aléatoire.
A force, j'ai un truc à peu prés exploitable pour approximer le temps moyen :
Avec toujours bougie, pour
bougie, pour 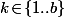 , le temps moyen
, le temps moyen 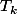 qu'il faut pour passer de l'état "
qu'il faut pour passer de l'état "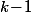 bougies éteintes" à l'état "
bougies éteintes" à l'état " bougies éteintes" est :
bougies éteintes" est : !(b-k)!}{i!(b-i)!}=\dfrac{1}{{b-1\choose k-1}}\sum_{i=0}^{k-1}{b\choose i}) (coefficients binomiaux)
(coefficients binomiaux)
Avec évidement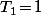 , mais le truc un peu moins évident, c'est qu'en fait
, mais le truc un peu moins évident, c'est qu'en fait 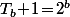 et, plus généralement,
et, plus généralement, 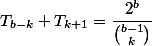 pour tout
pour tout 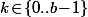
Le temps total moyen, c'est donc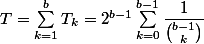 et, clairement,
et, clairement,  est proche de
est proche de 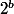 , et plus précisément de
, et plus précisément de ) .
.
Par exemple, pour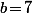 , on a
, on a
<br />=2^{7}\Big(1\!+\!\dfrac{1}{6}\!+\!\dfrac{1}{15}\!+\!\dfrac{1}{40}\Big)<br />=128\!\times\!\dfrac{151}{120}=\dfrac{2416}{15})
Avec toujours
Avec évidement
Le temps total moyen, c'est donc
Par exemple, pour
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
