Bonjour,
J'ai du faire une mauvaise manipulation en sauvegardant la brouillon de ma question sans l'envoyer.
je vous l'envoie donc maintenant.
------------------------------------------------------------------------
En examinant une suite particulière, je me suis posé
la question de son comportement, à savoir pourquoi à partir d'un certain rang
elle boucle, avec une périodicité constante (ici 3), autour des mêmes valeurs.
La suite définie sur le corps des réels est la suivante:
u(n)=((u(n-1)-p)*(u(n-2)-p))/(u(n-1)-u(n-2)-p) , p étant un paramètre défini
aussi sur les réels.
Il est facile de montrer que si à partir d'un certain rang
les valeurs de la suite se répètent avec une périodicité de 3,
alors cette périodicité se répète.
Dans la boucle périodique des valeurs successives x,y,z,t de la suite,il est
facile d'établir une relation entre y et x d'une part et entre z et x d'autre
part et enfin comme la périodicité est de trois, on x = t.
Le problème est de savoir pourquoi cette périodicité apparait
(comme une sorte de convergence)
quelques soient les valeurs de u(1) , u(2) et p.
Je vous remercie pour votre aide à venir.
Suite périodique
8 messages
- Page 1 sur 1
Re: suite périodique
vieuxpepe a écrit:Le problème est de savoir pourquoi cette périodicité apparait
(comme une sorte de convergence) quelques soient les valeurs de u(1) , u(2) et p.
Face à une relation dut type : pour tout
Et si, par exemple, l'expression de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: suite périodique
Bonjour
"Il est facile de montrer que si à partir d'un certain rang
les valeurs de la suite se répètent avec une périodicité de 3,
alors cette périodicité se répète.
Dans la boucle périodique des valeurs successives x,y,z,t de la suite,il est
facile d'établir une relation entre y et x d'une part et entre z et x d'autre
part et enfin comme la périodicité est de trois, on x = t."
Comme je l'ai dit en faisant x=t c'est-à-dire u(n+1) = u(n-2) on obtient les relations suivantes :
u(n-1) = (p^2)/(p-u(n-2) et
u(n) = p*(u(n-2) - p)/u(n-2).
A partir de ces relations, si u(2) =(p^2)/(p-u(1)), alors la périodicité 3 doit s'installer immédiatement.
Mais si l'égalité précédente n'est pas respectée dès le premier rang,
ALORS POURQUOI LES EGALITES APPARAISSENT-ELLES OBLIGATOIREMENT A PARTIR D'UN RANG
QUE L'ON NE CONNAIT PAS A L'AVANCE QUELQUES SOIENT LES VALEURS DE u(1) , u(2) , p ??????
là je sèche !!!
"Il est facile de montrer que si à partir d'un certain rang
les valeurs de la suite se répètent avec une périodicité de 3,
alors cette périodicité se répète.
Dans la boucle périodique des valeurs successives x,y,z,t de la suite,il est
facile d'établir une relation entre y et x d'une part et entre z et x d'autre
part et enfin comme la périodicité est de trois, on x = t."
Comme je l'ai dit en faisant x=t c'est-à-dire u(n+1) = u(n-2) on obtient les relations suivantes :
u(n-1) = (p^2)/(p-u(n-2) et
u(n) = p*(u(n-2) - p)/u(n-2).
A partir de ces relations, si u(2) =(p^2)/(p-u(1)), alors la périodicité 3 doit s'installer immédiatement.
Mais si l'égalité précédente n'est pas respectée dès le premier rang,
ALORS POURQUOI LES EGALITES APPARAISSENT-ELLES OBLIGATOIREMENT A PARTIR D'UN RANG
QUE L'ON NE CONNAIT PAS A L'AVANCE QUELQUES SOIENT LES VALEURS DE u(1) , u(2) , p ??????
là je sèche !!!
Re: suite périodique
Je comprend que dalle à ce que tu raconte : je viens de faire quelques tests (avec un tableur) et j'ai pas du tout constaté que la suite était cyclique quelque soient les valeurs de U(1), U(2) et p.vieuxpepe a écrit:ALORS POURQUOI LES EGALITES APPARAISSENT-ELLES OBLIGATOIREMENT A PARTIR D'UN RANG QUE L'ON NE CONNAIT PAS A L'AVANCE QUELQUES SOIENT LES VALEURS DE u(1) , u(2) , p ??????
là je sèche !!!
Ca semble même on ne peut plus exceptionnel que ce soit cyclique (ce qui n'a rien d'étonnant...).
Pa contre, il semblerais qu'assez fréquement, ça "tend" vers un 3-cycle, ce qui semblerais dire que l'itération triple admet un point fixe attractif (mais ça a rien de bien étrange non plus...)
C'est quoi qui te fait penser un truc pareil ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: suite périodique
D'abord Bonjour
et merci de ta patience.
J'ai fait moi-même des tests sur Excel jusqu'à au moins au rang n=2000 et à chaque fois (quelques soient les valeurs de u1 , u2 et p) ce 3-cycle apparait.
Essaye avec u1=2999 , u2=-512 et p=1.414114 , le 3-cycle apparait à partir de n=717,
ou bien avec u1=2.913188659 , u2=-1.333968521 et p=1.414114 , le 3-cycle apparait à partir de n=6
(car si on impose que u4 = u1 , alors u2=(p*p)/(p-u1) et donc u3=p*(u1-p)/u1 (condition qui apparait pour que u(n+1) = u(n-1) , c'est-à-dire pour que la périodicité soit égale à 3).
Bizarre , bizarre , vous avez dit bizarre ...
et merci de ta patience.
J'ai fait moi-même des tests sur Excel jusqu'à au moins au rang n=2000 et à chaque fois (quelques soient les valeurs de u1 , u2 et p) ce 3-cycle apparait.
Essaye avec u1=2999 , u2=-512 et p=1.414114 , le 3-cycle apparait à partir de n=717,
ou bien avec u1=2.913188659 , u2=-1.333968521 et p=1.414114 , le 3-cycle apparait à partir de n=6
(car si on impose que u4 = u1 , alors u2=(p*p)/(p-u1) et donc u3=p*(u1-p)/u1 (condition qui apparait pour que u(n+1) = u(n-1) , c'est-à-dire pour que la périodicité soit égale à 3).
Bizarre , bizarre , vous avez dit bizarre ...
Re: suite périodique
Vu qu'il n'y a que 15 décimales de précision avec les réels double précision des tableurs, on ne peut pas conclure.
Physiquement, un système vibratoire avec un état stable périodique peut être perturbé (Uo et U1) revient au bout d'un certain temps a ce même état stable périodique.
Physiquement, un système vibratoire avec un état stable périodique peut être perturbé (Uo et U1) revient au bout d'un certain temps a ce même état stable périodique.
Re: suite périodique
Bonjour à tous,
j'aimerais quand même savoir s'il existe une démonstration rigoureuse à cette convergence vers ce 3-cycle périodique, car il doit surement en exister une .
j'aimerais quand même savoir s'il existe une démonstration rigoureuse à cette convergence vers ce 3-cycle périodique, car il doit surement en exister une .
Re: suite périodique
Bien sûr, oui.
Tu considère la fonction\mapsto\big(\frac{(x-p)(y-p)}{x-y-p}\,;x\big)) , tu calcule
, tu calcule 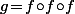 , tu cherche les points fixes de
, tu cherche les points fixes de  , tu calcule la différentielle de
, tu calcule la différentielle de  en ces points fixes et tu vérifie qu'ils sont effectivement (localement) attractifs.
en ces points fixes et tu vérifie qu'ils sont effectivement (localement) attractifs.
Par contre, vu la forme de f, LE truc super chiant si on veut un truc "bien propre", c'est de trouver un domaine D sur lequel f est défini et tel que f(D) soit contenu dans D pour pouvoir itérer sereinement le bidule.
Tu considère la fonction
Par contre, vu la forme de f, LE truc super chiant si on veut un truc "bien propre", c'est de trouver un domaine D sur lequel f est défini et tel que f(D) soit contenu dans D pour pouvoir itérer sereinement le bidule.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
