A la recherche de n^2=2^n

[morpho]

Bonjour,
Je me demande s'il n'existe pas d'autres entier que 2 qui verifient:
n^2=2^n ???

[alben]

Bonjour
Oui, il y en a un autre

[aviateurpilot]

Bonjour,
Je me demande s'il n'existe pas d'autres entier que 2 qui verifient:
n^2=2^n ???

pour

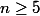
et pour
les seules solution sont 2 et 4

[RouJ]

Récurrence quand tu nous tiens...

[Thalès]

Comment pouvont nous démontrer qu'il existe une infinité de carrés parfaits de la forme 2^n?
Est-ce que l'équation x^y=y^x a pour solution le couple (2;4) seulement avec x différent de y?

[Nightmare]

Bonsoir,

"infinité de carrés parfaits de la forme 2^n"

C'est trivial: dès que n est pair, 2^n est un carré parfait.

[SimonB]

Est-ce que l'équation x^y=y^x a pour solution le couple (2;4) seulement avec x différent de y?

Oui, comme il résulte d'une simple étude de fonctions (la fonction , précisément).

[Thalès]

Oui je n'y avais pas pensé au départ