Bonjour,
C'est un sujet souvent abordé, et il me parait intéressant d'observer tout ce qui gravite autour de l'opération mathématique elle-même.
Bien-sûr cette discussion concerne surtout les utilisateurs directs et indirects de ces méthodes.
Pour qu'il n'y ait pas d'ambiguïté, je rappelle les hypothèses.
D'abord, j'appelle groupe un ensemble de quantités observées d'une chose. Bien souvent, le groupe sera un couple (x,y), ou un triplet (x,y,z), mais il pourra être plus grand. On conviendra par hypothèses que les différents éléments d'un groupe sont indépendants, c'est à dire non liés.
Une liste ou série est un ensemble de groupes en nombre limité, mais suffisant.
Le but de l'opération est de déterminer une fonction qui peut résumer l'ensemble de la série. On obtient ainsi ce qu'on appelle souvent un modèle mathématique.
Toute correction ou précision de cette définition constitue le premier but de cette discussion : "de quoi s'agit-il".
A propos des régressions
7 messages
- Page 1 sur 1
Bonjour,
je donne une définition mathématique assez générale du problème de regression.
Soit un ensemble de couples_{i=1,...,N}) , où chaque
, où chaque  est élément de
est élément de  (ce qui signifie que chaque x_i est en fait un ensemble de n valeurs réelles), et chaque
(ce qui signifie que chaque x_i est en fait un ensemble de n valeurs réelles), et chaque  est élément de
est élément de 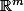 .
.
Moralement le problème de régression consiste à trouver, dans une classe de fonction donnée, la fonction f qui représente le mieux le lien entre x_i et y_i.
Pour cela il faut définir :
- la classe de fonction F dans laquelle on cherche notre relation
- ce que signifie "représenter le mieux"
Représenter le mieux en maths cela signifie minimiser une distance. Ici on parle donc de minimiser la distance entre les différentes prédictions,...,f(x_N)),(y_1,...,y_N))) . Le problème s'écrit donc
. Le problème s'écrit donc
,Y)) où f(X)=(f(x_1),...,f(x_N)) et Y= (y_1,...,y_N).
où f(X)=(f(x_1),...,f(x_N)) et Y= (y_1,...,y_N).
Supposons pour simplifier que m=1, c'est à dire que les f(x_i) et les y_i sont des réels. Dans ce cas l'un des choix les plus classiques de distance sur R^N sera celle issue de la norme 2 :
,Y)=\sum_{i=1}^N (f(x_i)-y_i)^2.) Ainsi le problème sera le fameux problème des moindres carrés. On peut aussi considérer d'autres distances issues de normes :
Ainsi le problème sera le fameux problème des moindres carrés. On peut aussi considérer d'autres distances issues de normes :
,Y)=\sum_{i=1}^N |f(x_i)-y_i|.)
,Y)=\max_{i=1,..,N} |f(x_i)-y_i|.)
Reste un point important : ici la variable sur laquelle on minimise est une fonction, soit a priori un truc qui vit dans un espace de dimension infini. Si on ne mets pas de contraintes fortes sur ces fonctions il est facile de trouver une fonction (même continue ou C^\infty) qui donne une distance nulle. Quasi-systématiquement on souhaite que la fonction f puisse être paramétrée par un nombre fini de paramètres. Dans un autre fil Dlzlogic a donné un certain nombre d'exemples de classe de fonctions. J'en rappelle une ou deux (par simplicité je suppose aussi que n=1) ici pour être complet :
Ensemble des fonctions linéaires :
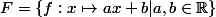
Fonction polynomiale de degré donné (par exemple 3)
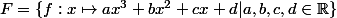
Fonction puissance
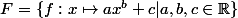
etc...
Ainsi la minimisation de,Y)) devient une minimisation sur un nombre fini de paramètres. On peut donc appliquer des algo de minimisation classique (avec un peu de chance la distance choisie est convexe et différentiable et on peut appliquer une méthode de Gradient ou de Newton). Si la norme est la norme 2 et que l'on prends pour F les fonction linéaires on a des formules explicites.
devient une minimisation sur un nombre fini de paramètres. On peut donc appliquer des algo de minimisation classique (avec un peu de chance la distance choisie est convexe et différentiable et on peut appliquer une méthode de Gradient ou de Newton). Si la norme est la norme 2 et que l'on prends pour F les fonction linéaires on a des formules explicites.
Le choix de la classe de fonction F ne relève pas vraiment des mathématiques. Il doit être guidé par :
- la connaissance de la physique du phénomène étudié
- une obvservation globale du phénomène
- éventuellement une comparaison de différentes classes de fonctions. Dans ce cas il faut faire attention à ne pas mettre trop de paramètres par rapport au nombre de données. En effet, pour les polynomes par exemple, il y a toujours un polynome de degré n qui passe exactement par n points, par contre son comportement n'est pas forcément un qui représente bien le lien entre les x et les y.
P.S : si des choses ne sont pas claires je modifirais le message, et si des gens conteste le framework je donnerais un lien ou deux.
je donne une définition mathématique assez générale du problème de regression.
Soit un ensemble de couples
Moralement le problème de régression consiste à trouver, dans une classe de fonction donnée, la fonction f qui représente le mieux le lien entre x_i et y_i.
Pour cela il faut définir :
- la classe de fonction F dans laquelle on cherche notre relation
- ce que signifie "représenter le mieux"
Représenter le mieux en maths cela signifie minimiser une distance. Ici on parle donc de minimiser la distance entre les différentes prédictions
Supposons pour simplifier que m=1, c'est à dire que les f(x_i) et les y_i sont des réels. Dans ce cas l'un des choix les plus classiques de distance sur R^N sera celle issue de la norme 2 :
Reste un point important : ici la variable sur laquelle on minimise est une fonction, soit a priori un truc qui vit dans un espace de dimension infini. Si on ne mets pas de contraintes fortes sur ces fonctions il est facile de trouver une fonction (même continue ou C^\infty) qui donne une distance nulle. Quasi-systématiquement on souhaite que la fonction f puisse être paramétrée par un nombre fini de paramètres. Dans un autre fil Dlzlogic a donné un certain nombre d'exemples de classe de fonctions. J'en rappelle une ou deux (par simplicité je suppose aussi que n=1) ici pour être complet :
Ensemble des fonctions linéaires :
Fonction polynomiale de degré donné (par exemple 3)
Fonction puissance
etc...
Ainsi la minimisation de
Le choix de la classe de fonction F ne relève pas vraiment des mathématiques. Il doit être guidé par :
- la connaissance de la physique du phénomène étudié
- une obvservation globale du phénomène
- éventuellement une comparaison de différentes classes de fonctions. Dans ce cas il faut faire attention à ne pas mettre trop de paramètres par rapport au nombre de données. En effet, pour les polynomes par exemple, il y a toujours un polynome de degré n qui passe exactement par n points, par contre son comportement n'est pas forcément un qui représente bien le lien entre les x et les y.
P.S : si des choses ne sont pas claires je modifirais le message, et si des gens conteste le framework je donnerais un lien ou deux.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Bonjour Sylviel,
J'ai tout lu, mais ce n'était pas vraiment le sujet de la discussion.
Tu parles de résolution du problème, j'ai ouvert cette discussion à propos d'utilisation, nécessité de se poser le problème, et en particulier, j'aimerais bien des exemples d'utilisation.
Pour être plus précis, la résolution est un affaire de matheux, d'informaticiens, ce n'est pas le but de ma question.
J'ai tout lu, mais ce n'était pas vraiment le sujet de la discussion.
Tu parles de résolution du problème, j'ai ouvert cette discussion à propos d'utilisation, nécessité de se poser le problème, et en particulier, j'aimerais bien des exemples d'utilisation.
Pour être plus précis, la résolution est un affaire de matheux, d'informaticiens, ce n'est pas le but de ma question.
Dlzlogic a écrit:Bonjour Sylviel,
J'ai tout lu, mais ce n'était pas vraiment le sujet de la discussion.
Tu parles de résolution du problème, j'ai ouvert cette discussion à propos d'utilisation, nécessité de se poser le problème, et en particulier, j'aimerais bien des exemples d'utilisation.
Pour être plus précis, la résolution est un affaire de matheux, d'informaticiens, ce n'est pas le but de ma question.
http://en.wikipedia.org/wiki/Nonlinear_regression
http://www.graphpad.com/manuals/prism4/regressionbook.pdf
http://www.minitab.com/fr-FR/training/articles/articles.aspx?id=9030&langType=1036
http://www-stat.stanford.edu/~jtaylo/courses/stats203/notes/nonlinear.pdf
http://www.iasri.res.in/ebook/EB_SMAR/e-book_pdf%20files/Manual%20IV/1-Nonlinear%20Regression.pdf
exemples in french:
http://perso.univ-rennes1.fr/bernard.delyon/regression.pdf
http://spiral.univ-lyon1.fr/files_m/M4922/Files/370377_4566.pdf
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Un exemple que j'ai donné en TP d'optimisation :
On veut faire une cartographie du fonds de l'Océan. Pour cela on dispose d'un bateau qui laisse traîner derrière lui un cable avec un sonar et des capteurs. Le sonar emet à intervalle régulier un salve et les récepteurs enregistre le temps mis par l'onde pour revenir, on en déduit donc la distance parcourue par l'onde entre l'emetteur et le recepteur.
Pour modéliser le fonds de l'océan on utilise des splines (Polynomes par morceaux de degré 3 qui sont C²). Pour une spline donnée on peut calculer les temps théoriques pour chaque trajet.
Dans le formalisme général cela donne :
- les x_i sont les couples (position d'émission, position de réception)
- les y_i sont les temps de parcours
- l'ensemble F est l'ensemble des temps mis pour chaque onde en fonction de la spline qui représente le fond paramétrées par un nombre fini de paramètres.
- la distance choisie est celle de la norme 2 (i.e minimisation des moindres carrés).
On veut faire une cartographie du fonds de l'Océan. Pour cela on dispose d'un bateau qui laisse traîner derrière lui un cable avec un sonar et des capteurs. Le sonar emet à intervalle régulier un salve et les récepteurs enregistre le temps mis par l'onde pour revenir, on en déduit donc la distance parcourue par l'onde entre l'emetteur et le recepteur.
Pour modéliser le fonds de l'océan on utilise des splines (Polynomes par morceaux de degré 3 qui sont C²). Pour une spline donnée on peut calculer les temps théoriques pour chaque trajet.
Dans le formalisme général cela donne :
- les x_i sont les couples (position d'émission, position de réception)
- les y_i sont les temps de parcours
- l'ensemble F est l'ensemble des temps mis pour chaque onde en fonction de la spline qui représente le fond paramétrées par un nombre fini de paramètres.
- la distance choisie est celle de la norme 2 (i.e minimisation des moindres carrés).
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Bonjour,
En terme pratiques je pense que la question n'est pas tant dans la régression elle-même, qui est "seulement" un algo type Newton/Amibe/autre qui tourne que la question préalable du contexte de la modélisation qui va orienter grandement le choix.
Une fois qu'on lance la régression c'est qu'on a répondu aux questions suivantes :
- Veut-on décrire seulement de manière analytique une courbe expérimentale ou veut-on expliquer un phénomène avec une mécanique sous-jacente (calibration de modèle) ? Dans le second cas, des classes de fonctions de régressions seront prédéterminées/guidés par les modèles "physiques" sous-jacent.
- Que veut-on faire du résultat ? Est-ce purement pour trouver la meilleure courbe à de stockage facilité de données/éliminations de points aberrants, ou veut-on réutiliser ensuite cette courbe dans des calculs (possiblement différentiels), ce qui apportera des contraintes de régularités à respecter plus ou moins stricte.
- Nos observations sont-elles toutes aussi importantes/fiables ? Cela permettra de pondérer les observations dans la fonction d'erreur selon le degré d'importance/fiabilité.
A priori si toutes ces questions ont été répondues, on a plutôt bien cadré le problème et on voit ce que l'on peut faire ou non.
J'aurais bien des exemples en mathématiques financières mais ils sont un peu obscurs vus de l'extérieur ... mais j'ai rencontré les différents cas de figures que je décris plus haut.
Damien
En terme pratiques je pense que la question n'est pas tant dans la régression elle-même, qui est "seulement" un algo type Newton/Amibe/autre qui tourne que la question préalable du contexte de la modélisation qui va orienter grandement le choix.
Une fois qu'on lance la régression c'est qu'on a répondu aux questions suivantes :
- Veut-on décrire seulement de manière analytique une courbe expérimentale ou veut-on expliquer un phénomène avec une mécanique sous-jacente (calibration de modèle) ? Dans le second cas, des classes de fonctions de régressions seront prédéterminées/guidés par les modèles "physiques" sous-jacent.
- Que veut-on faire du résultat ? Est-ce purement pour trouver la meilleure courbe à de stockage facilité de données/éliminations de points aberrants, ou veut-on réutiliser ensuite cette courbe dans des calculs (possiblement différentiels), ce qui apportera des contraintes de régularités à respecter plus ou moins stricte.
- Nos observations sont-elles toutes aussi importantes/fiables ? Cela permettra de pondérer les observations dans la fonction d'erreur selon le degré d'importance/fiabilité.
A priori si toutes ces questions ont été répondues, on a plutôt bien cadré le problème et on voit ce que l'on peut faire ou non.
J'aurais bien des exemples en mathématiques financières mais ils sont un peu obscurs vus de l'extérieur ... mais j'ai rencontré les différents cas de figures que je décris plus haut.
Damien
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
