à propos des nombres complexe
14 messages
- Page 1 sur 1
à propos des nombres complexe
Bonsoir,
dans le cours on dit que chaque proprieté de l'ensemble IR est valide dans l'ensemble des nombres complexes ..mais en voyant le nombre i on va constater que le carré d'un nombre est negatif or c'est c'est posetif dans IR...ça veut dire il y un probleme de classement ici..donc j'ai besoin de qlq'un à m'expliquer cette contradiction..et s'il ya des sources de recherche pour ce sujet Je vous serais reconnaissant de bien
dans le cours on dit que chaque proprieté de l'ensemble IR est valide dans l'ensemble des nombres complexes ..mais en voyant le nombre i on va constater que le carré d'un nombre est negatif or c'est c'est posetif dans IR...ça veut dire il y un probleme de classement ici..donc j'ai besoin de qlq'un à m'expliquer cette contradiction..et s'il ya des sources de recherche pour ce sujet Je vous serais reconnaissant de bien
Pour moi je n'applique les prop des IR sur les nombres complexes si seulement si le nombre complexe est un réal car à la fin un autre exemple de contradiction c'est les identités remarquables (a+ib)²=a²-b²+i2ab
alors si le nombre complexe était real on va pas avoir ce resultat donc vrmt les nombre complexe sans i vont etre pluuuuus simple :cry: (je veux en faite savir qu'est la personne qu' découvert ces nombres :mur: :mur: )
alors si le nombre complexe était real on va pas avoir ce resultat donc vrmt les nombre complexe sans i vont etre pluuuuus simple :cry: (je veux en faite savir qu'est la personne qu' découvert ces nombres :mur: :mur: )
ooops
bein merci pour vos reactions mais j'ai pas trouvé la bonne reponse...moi je cherche comment prouver la contradiction entre les proprietes de IR et C et par consequent montrer que la regle est fausse
Nb
bein maint je derrige le parole aux membres "complexes" lol puisque c'est notre sujet lol...enfin vous etes genials les gars merci pour vos reactions et tt
mon but??
je cherche a refuter cette regle qui dit chaque propriete de IR est valide dans l"ensemble des nombres complexe ..en citant l"ex de classement t'as compris??
Oui, dire que toutes les propriétés de R sont vraies dans C est un peu abusé, il faudrait préciser.
Pour ce qui est des carrés négatifs, c'est une raison qui explique la construction du corps des complexes. En fait, on a remarqué en manipulant des équations que si l'on considérait des racines carrés de nombres négatifs, on aboutissait à des résultats réels (je cite l'exemple histoire de la méthode de Tartaglia pour la résolution des équations du 3ème degré, Bombelli a dû introduire le nombre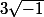 ).
).
On a donc créé un surcorps de R, les complexes, où l'on peut considérer des carrés négatifs. On se rend vite compte que les complexes sont utiles partout, peut être même plus que les réels (d'où la maxime d'Hadamard citée plus haut).
Pour ce qui est des carrés négatifs, c'est une raison qui explique la construction du corps des complexes. En fait, on a remarqué en manipulant des équations que si l'on considérait des racines carrés de nombres négatifs, on aboutissait à des résultats réels (je cite l'exemple histoire de la méthode de Tartaglia pour la résolution des équations du 3ème degré, Bombelli a dû introduire le nombre
On a donc créé un surcorps de R, les complexes, où l'on peut considérer des carrés négatifs. On se rend vite compte que les complexes sont utiles partout, peut être même plus que les réels (d'où la maxime d'Hadamard citée plus haut).
Nightmare a écrit:On a donc créé un surcorps de R, les complexes
Même si à l'époque on ne disait pas "surcorps" :happy2:
Notons tout de même que cette création a eu lieu très tard dans l'histoire des mathématiques et qu'elle a suscité de nombreuses difficultés d'ordre épistémologique (tout comme les nombres négatifs, qui "ne représentent rien de concret").
idriss_alfred a écrit:je cherche a refuter cette regle qui dit chaque propriete de IR est valide dans l"ensemble des nombres complexe ..en citant l"ex de classement t'as compris??
Il vrai que beaucoup de propriétés de IR sont valables pour C aussi, mais c'est, comme tu le remarques, faux de généraliser
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
