Extensions du corps des réels.

[vincentroumezy]

Salut à tous.
Je me demandais, après avoir entendu parlé, et meme plus des quaternions, octonions et sedénions, je me demandais s'il existait une infinité d'extensions du corps des réels, qui ne soient pas nécéssairement commutatifs.

[Luc]

Hello,

je me permets d'up ce fil.
La question d'extension de corps est très intéressante en algèbre, et peut être vue comme une conséquence de l'existence, dans certains cas, de polynômes (par exemple à coefficients réels) qui n'admettent pas de racine (par exemple pas de racine réelle). n'admet pas de racine réelle. Le "plus petit corps" contenan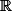t et est le corps des nombres complexes, a un isomorphisme près.
Je crois qu'on peut construire une infinité de corps non commutatifs (avec un produit particulier sur l'anneau des séries formelles à une indéterminée d'un corps commutatif). Des connaisseurs peuvent confirmer?

Luc

Salut à tous.
Je me demandais, après avoir entendu parlé, et meme plus des quaternions, octonions et sedénions, je me demandais s'il existait une infinité d'extensions du corps des réels, qui ne soient pas nécéssairement commutatifs.

[Skullkid]

Bonjour, normalement quand on parle d'extension on sous-entend la commutativité. R et C sont les seules extensions algébriques de R (c'est-à-dire dont tous les éléments sont racine d'un polynôme à coefficients dans R). Les quaternions forment un corps non commutatif donc ils ne comptent pas comme extension de R (ni de C), et les octonions et sédénions ne forment pas un corps du tout. Si on veut une extension de R plus grosse que C, on est obligé de prendre une extension transcendante, comme par exemple le corps des fractions rationnelles à une indéterminée à coefficients réels, ou certains ensembles auxquels je ne connais rien comme les hyperréels... Mais rien n'empêche de construire des anneaux plus gros que les sédénions (mais les noms commenceraient probablement à devenir moches, genre "trigintibinions"...)

Je ne sais pas ce qu'il en est pour les séries formelles, je ne connais que leur structure classique en anneau. Tu te rappelles à quoi ressemblait ce produit particulier sur les séries, Luc ?

[Luc]

En revanche il y a plein d'extensions algébriques non triviales de : les extensions quadratiques, les nombres constructibles à la règle et au compas... et les nombres algébriques (ie la clôture algébrique de )

Pour les séries formelles, je parlais plus précisément des séries formelles de Laurent de la forme ou les sont tous nuls sauf un nombre fini, à coefficients dans un corps donné. On peut le munir d'une structure d'anneau et même de corps avec le produit , qui est commutatif (c'est le produit de Cauchy). Mais j'ai lu qu'on pouvait en fait le munir d'une structure de corps non commutatif (en anglais : skew field ou non commutative division ring) si on définit un autre produit, dont je n'arrive pas à avoir la définition explicite, mais qui utilise un automorphisme de corps donné ,)

[vincentroumezy]

Merci pour ces précisions.