Rang d'infini des hyper réels

[lulu math discovering]

Salut.

Si vous avez lu le titre de ce topic, vous aurez compris ce qui m'interroge.
A lire si vous connaissez un peu les rangs d'infini de Cantor.

Le rang d'infini aleph 0 correspond notamment aux nombres entiers. On peut les représenter comme des points à placer sur une droite.
Le rang d'infini aleph 1 correspond aux réels qu'on peut bien sur représenter sur une droite (des réels).

Une façon que je trouve très intuitive de se rendre compte de la barrière infranchissable qu'est le changement de rang, :id: c'est que vous aurez beau toujours rajouter des points sur votre droite, ça ne vous permettra jamais de tracer une droite pleine.
Prolonger l'infini de rang 0 ne vous permettra jamais d'atteindre le suivant.

J'invite les anglophones à regarder cette vidéo où ils représentent les hyper réels avec un morceau de droite, mais qui serait inaccessible à la droite des réels (en souhaitant prolonger celle-ci).

Les hyper réels correspondraient-ils à aleph 2 ?? :id:

Si vous avez eut le courage de lire ce pavé et que vous avez compris, merci de me dire ce que vous en pensez !!! :++:

[L.A.]

Bonsoir,

je dis peut-être une bêtise, mais est-ce ces hyperréels ne seraient pas en bijection avec l'ensemble des fractions rationnelles R(X) muni d'une relation d'ordre particulière ? (l'indéterminée X étant identifiée avec le K de la vidéo)

[lulu math discovering]

Euh... Si tu pouvais développer ? J'ai peur de ne pas avoir compris.
Enfin si, je comprends les termes employés, mais pas le sens de ta phrase.

[L.A.]

Encore une fois je découvre les notions avec la vidéo, donc il est possible que je dise n'importe quoi...

Mais à ce que j'ai pu comprendre, tes hyperréels forment un corps ordonné (disons R') et qui vérifie :
- R' contient R en tant que sous-corps ;
- R' contient un élément K qui est un majorant de la partie R.

On peut envisager le morphisme de R-algèbres de R(X) dans R' qui à X associe K. Si celui-ci est surjectif par exemple, le cardinal de R' n'est pas plus grand que celui de R(X). Bien sûr R' peut aussi être beaucoup plus grand que l'image de R(X), a priori rien ne l'empêche si R' contient beaucoup d'éléments comme K indépendants entre eux, mais dans ce cas le cardinal de R' peut aussi être "arbitrairement" grand.

De toute façon, l'image de R(X) dans R' a aussi les deux propriétés ci-dessus, ce n'est peut-être pas la peine d'aller chercher plus loin...

EDIT : et j'avoue au passage que j'ignore si le cardinal de R(X) est plus grand que celui de R. :doh:

[lulu math discovering]

Tu te demandes donc comme moi si le cardinal est le même ou non c'est ça ? (traduction)

[L.A.]

Je suggère que pour connaître le cardinal de ces hyperréels, il suffit grosso-modo de connaître le cardinal des fractions rationnelles R(X). :zen:

[lulu math discovering]

Attends attends... tu parles des nombres rationnels là ?
Parce que je t'arrêtes tout de suite, ils ont le même cardinal que les entiers.

[Skullkid]

Bonsoir, l'ensemble des hyperréels a le même cardinal que celui des réels, c'est-à-dire 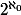(dire que le cardinal de est 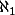revient à admettre l'hypothèse du continu). Ça peut se voir en construisant les hyperréels comme classes d'équivalence de suites de réels, le K de la vidéo correspondant à la classe d'une certaine suite qui tend vers l'infini.

En considérant uniquement les fractions rationnelles tu risques de manquer les nombres du type sqrt(K) ou K^K. Cela dit, les hyperréels sont bien en bijection avec les fractions rationnelles réelles, c'est juste qu'identifier l'indéterminée à K ne fournit qu'une injection.

[nodjim]

Une petite énigme philosophique:
Dieu, qui est tout puissant créé un bâtiment curieux: une seule porte d'entrée, et derrière cette porte, une salle avec 9 autres portes. Derrière chacune des portes, 1 salle avec 10 autres portes de sortie. Et ainsi de suite à l'infini (1 porte d'entrée, 10 de sorties). Ce créateur infatiguable créé une infinité d'hommes pour visiter ce bâtiment. Chaque homme y entrant doit se déplacer infiniment de salle en salle, sans jamais revenir en arrière ni s'arrêter. On ne doit trouver qu'un seul homme par salle, et pourtant Dieu se demande s'il peut compter plus d'hommes que de salles.
Qu'en pensez vous ?

[alphamethyste]

Salut mais Il ne devrait pas se le demander pourtant car il peut mettre l'ensemble des salles en bijection avec l'ensemble des humains

avec et

ceci dit ça marche aussi si Dieu crée une quantitée
d'humains avec et qu'il crée salles

[L.A.]

Ça peut se voir en construisant les hyperréels comme classes d'équivalence de suites de réels, le K de la vidéo correspondant à la classe d'une certaine suite qui tend vers l'infini.

Tu peux être plus précis s'il te plait ?

En considérant uniquement les fractions rationnelles tu risques de manquer les nombres du type sqrt(K) ou K^K. Cela dit, les hyperréels sont bien en bijection avec les fractions rationnelles réelles, c'est juste qu'identifier l'indéterminée à K ne fournit qu'une injection.

Il y a donc un log et une exponentielle sur ces choses-là ?

[nodjim]

@ Alphamétiste:
On peut facilement modéliser les hommes comme des réels et les salles comme des nombres décimaux.

[Doraki]

Il y a une définition quelque part dans la vidéo ?

[lulu math discovering]

Non il n'y a pas de définition. Une mathématiciene explique juste le principe des hyper réels et les manipule/représente un peu avec la droite des réels.

Mais skullkid pourrais tu etre plus précis quand à l'explication du fait que les hyper réels ont le meme cardinal que les réels ?

[Skullkid]

Une construction est donnée sur Wiki. L'idée de base est que les suites qui tendent vers 0 vont représenter des nombres infinitésimaux et les suites qui tendent vers l'infini vont représenter des infiniment grands. La partie technique consiste à assigner une valeur aux suites oscillantes et à s'assurer que l'ordre total des réels se prolonge bien (il s'agit de restreindre la comparaison entre deux suites à certains ensembles d'indices "importants" qu'on choisit au préalable ; par exemple signifie "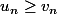 pour tous les n dans un ensemble important") mais sinon c'est assez similaire à la construction des réels par les suites de Cauchy rationnelles.

Pour ce qui est du cardinal,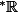 contient une copie de (via les suites constantes) et est plus petit que 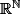, qui est lui-même équipotent à .

Dans la vidéo ils adoptent une approche axiomatique qui consiste à supposer qu'il existe un nombre infiniment grand et que si une propriété est vraie pour tous les réels, alors elle se traduit immédiatement en une propriété vraie pour tous les hyperréels.

[zygomatique]

salut

et si tu simplement ?

[Skullkid]

Où veux-tu en venir ? Si c'est une histoire de nom, tu peux appeler ton infiniment grand "axiomatique" comme tu veux (du moment qu'il a pas le même nom qu'un réel), m'enfin j'éviterais quand même de l'appeler vu que ça impliquerait des trucs du genre 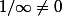ou 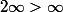, qui personnellement me font un peu tiquer.

Si par contre tu sous-entends qu'on a déjà, dans un contexte plus simple que celui des hyperréels, un objet qui s'appelle et qui satisfait tout ce qu'on demande à K, alors je le connais pas. Par exemple, le de la droite réelle achevée ne convient pas puisqu'on ne peut pas lui étendre les propriétés des réels.

[lulu math discovering]

Idem. Ca me fait mal de dire K=+infini. Je préfère dire que K est un nombre tel que tout x de R est tel que x<K (si bien sur on ne considère pas les nombres K+1, 2K ...).

[lulu math discovering]

Bon. J'ai quand meme pas envie de laisser ce topic mourir, alors je voudrais savoir : comment on prouve que les entiers ont un rang d'infini différent de celui des réels ?

[Skullkid]

Cherche "argument diagonal de Cantor"