Un exercice bien diffc
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
Houda.9rayti
- Membre Relatif
- Messages: 132
- Enregistré le: 30 Sep 2010, 12:48
-
 par Houda.9rayti » 30 Sep 2010, 12:50
par Houda.9rayti » 30 Sep 2010, 12:50
Bonjour :)
x et y sont des nombres de R
montrez que
p1 : \/¯(x-1) + 2\/¯(y-4) = (x+y)/2 <=> x=2 et y=
Merci encore !
ps : j'ai réussi a démontrer "<=" ( la partie la plus facile )si vous me comprenez. Il vous suffit de montrez que =>

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 30 Sep 2010, 12:54
par Olympus » 30 Sep 2010, 12:54
Salut !
C'est faux, ou alors c'est plutôt

et pas

.
-
Houda.9rayti
- Membre Relatif
- Messages: 132
- Enregistré le: 30 Sep 2010, 12:48
-
 par Houda.9rayti » 30 Sep 2010, 13:01
par Houda.9rayti » 30 Sep 2010, 13:01
effectivement , je dois encore rectifier !
je reprends alors
\/¯(x-1) + 2\/¯(y-4) = (x+y)/2 <=> x=2 et y=8
et merci !

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 30 Sep 2010, 13:06
par Olympus » 30 Sep 2010, 13:06
Oki, donc d'abord on a

et

.
Donc il existe deux réels positifs

et

tels que
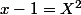
et
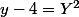
.
Donc
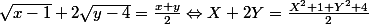
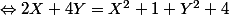
^2 + \left(X-1\right)^2 = 0)
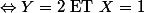
Et tu pourras continuer . L'équivalence est conservée, donc pas la peine de vérifier .
-
Houda.9rayti
- Membre Relatif
- Messages: 132
- Enregistré le: 30 Sep 2010, 12:48
-
 par Houda.9rayti » 30 Sep 2010, 13:11
par Houda.9rayti » 30 Sep 2010, 13:11
merci beaucoup beaucoup beaucoup
tu m'as sauvé la vie. Cet question ci dessus me rendait dingue
merci, c'est si claire maintenant :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités
