Demonstration a^0 = 1 (a non nul)

par **maxence6** » 08 Fév 2010, 22:10

Bonjour, Bonsoir je recherche la démonstration de a^0 = 1.

J'ai commencé par faire un exemple:

Ecriture décimale:
10^3 x 10^-3 = 10^3+(-3) = 10^0 = 1
Ecriture fractionnaire:
1000/1 x 1/ 1000 = 1000/1000 = 1
donc 10° = 1

mais ce n'est pas une véritable démonstration, si quelqu'un pourrait me la montré.

par **Nightmare** » 08 Fév 2010, 22:14

Bonjour,

c'est une convention, un produit de zéro éléments vaut 1 (neutre pour la multiplication), tout comme une somme de 0 élément vaut 0 (neutre pour l'addition).

par **maxence6** » 08 Fév 2010, 22:17

D'accord donc il n'y a pas de démonstration ?

par **Nightmare** » 08 Fév 2010, 22:19

Bein non, c'est une convention. On aurait pu poser

mais alors beaucoup d'énoncé sur les puissances ne seraient plus vrai en 0 (c'est possible par contre que d'autre le soient alors qu'ils ne l'étaient pas avant)

par **maxence6** » 08 Fév 2010, 22:27

Ok merci, bonne soirée

par **zenko** » 08 Fév 2010, 22:38

Peut-être une piste :

avec n,p non nul
d'où

par **Ben314** » 08 Fév 2010, 23:01

zenko a écrit:Peut-être une piste :
avec n,p non nul
d'où

Tu as parfaitement raison, c'est une piste... pour expliquer que la convention

est "logique".

Mais, pour que ce soit une "preuve", il faudrait avoir démontré avant que

pour tout p,q, y compris pour q=0.
Or, pour montrer que cette formule est valable pour q=0, il faut préalablement.... avoir défini

.

Résumé : TRES BON argument pour justifier la convention, mais ce n'est pas une preuve...

par **Anonyme** » 09 Fév 2010, 08:41

Je n'ai pas trop compris cette histoire de convention.

Pourquoi cela n'est pas une preuve ?
Dans celle ci pas besoin de définir

par **ffpower** » 09 Fév 2010, 09:04

Comment tu veux prouver ce que vaut un truc sans l'avoir défini avant? ;)

Dis moi donc ce que vaut "trucmuche(3)" sans que je te définisse "trucmuche" ^^

par **Ben314** » 09 Fév 2010, 09:07

Dans cette "preuve", tu as utilisé la formule

(avec

et

).
Comment fait tu pour prouver cette formule ?

par **maxence6** » 09 Fév 2010, 09:10

Mais je crois peut être avoir un autre argument.
a^b et a^-b sont inverse...

Et tout le monde sais que le produit de deux nombres inverses fait 1.

par **ffpower** » 09 Fév 2010, 09:13

maxence6 a écrit:Mais je crois peut être avoir un autre argument.
a^b et a^-b sont inverse...

Et tout le monde sais que le produit de deux nombres inverses fait 1.

Ca aussi c est par définition de a^{-b}..Et ok le produit fait 1 ( par définition ), mais tu ne risques pas de prouver que ca fait aussi a^0 si tu connais pas la definition de a^0.
( d'ailleurs en théorie, en convient que a^{-n}=1/a^n seulement après avoir convenu que a^0=1..)

par **maxence6** » 09 Fév 2010, 09:18

C'est vrai j'avais pas pensé à ça :hein:

par **Anonyme** » 09 Fév 2010, 09:23

ffpower a écrit:Comment tu veux prouver ce que vaut un truc sans l'avoir défini avant?

Mais si je défini

comme étant égale a

Je n'aurais plus a le calcule donc a le prouver.
Je ne suis pas très convaincu par ce que vous dite.

Note: Je dis certainement des connerie, mais j'étais tellement convaincu que ...

par **ffpower** » 09 Fév 2010, 09:32

C'est la démarche inverse qu'il faut faire..On sait définir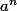

a priori pour n entier strictement positif, puis montrer la formule

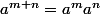qui est donc valable pour m,n entiers STRICTEMENT positif. Aprés alors on a envie de savoir quelle valeur donner à

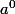. On décide alors que dorénavant,

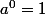, et aprés, on prouve qu avec cette définition, on a encore la formule

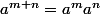qui est valide pour m,n entiers positifs ( plus strictement )..Puis après on décrete que

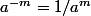, et on prouve alors que

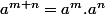est vraie pour m,n entiers relatifs..(puis aprés on peut aussi définir

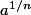, mais on va s arrêter là

)

par **Ben314** » 09 Fév 2010, 09:48

Comme j'ai (presque) rien d'autre à faire, voilà ce que l'on peut écrire (En supposant évidement qu'au départ, on ne connait absolument rien aux puissances)

Définition 1 : Pour tout réel

et tout naturel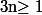

on définit

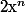par :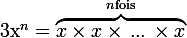

Remarque : Cette définition ne définit absolument pas

ni

Théorème 1 : Pour tout réel

et tout

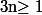et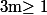

on a :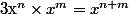

Preuve :

Remarque : Pour le moment, ce théorème n'est évidement vrai que pour

et

vu qu'on a pas de définition de

pour

!!!!

Arrivé à ce point, on aimerait définir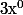

et

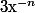(pour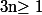

) de façon à ce que le théorème 1 ci dessus reste vrai pour tout entier relatif.
Si une telle définition existe, on doit avoir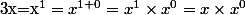

donc, si

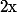est non nul (simplification par

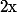) on doit définir

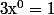si on veut que le théorème 1 reste vrai.
De même, on voudrait que

donc, pour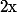

non nul, on doit définir

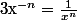si on veut que le théorème 1 reste vrai.

Définition 2 : Pour tout réel

non nul et tout naturel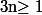

on définit

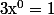et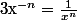

Théorème 2 : Pour tout réel

non nul et tout

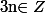et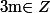

on a :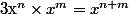

Preuve : On distingue tout les cas possibles :
- Si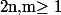

déjà fait.
- Si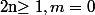

alors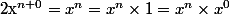

.
.
.

Edit : grillé par ffpower (faut dire que j'ai mis 3 plombes à taper tout ça !!!)

par **Anonyme** » 09 Fév 2010, 10:10

Merci beaucoup Ben et ffpower !

J'ai enfin compris. :zen:

Autre chose: Comment a -t on défini les puissance rationnelles et irrationnelles ?
(surtout les irrationnelles) ?

Cela m'intéresse. Vous connaissez des cours (sur le net) qui expliquent bien les puissance a partir de zéro ? (Je ne veux pas vous embêter a m'expliquer le tout quand même :zen: )

@ Ben : Tres belle mis en page. Tu maitrise le

(Je sais même pas comment faire pour écrire le logo de Latex :briques: )

par **Ben314** » 09 Fév 2010, 10:44

Pour le mimeTeX utilisé ici, j'ai mis cette page :
http://www.forkosh.dreamhost.com/source_mimetexmanual.html#preview
dans mes favoris et je fait des copier-coller des exemples qu'il donnent...

Pour les puissance rationelle on peut partir un peu comme comme pour les négatifs : pour deux entiers n et m on démontre que

et on aimerais définir

pour un quotient p/q en se débrouillant pour que la formule sur les entiers reste vraie.
On aimerait donc que

.
Cela conduit a prendre comme définition de

la racine q-ième de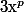

(pour x>0)
Il faut vérifier que cette définition a un sens car le même quotient a plusieurs écriture. Par exemple 3/5=9/15 donc il faut vérifier que la racine cinquième de

est bien égale à la racine quinzième de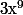

.
Ensuite, on démontre que les puissances rationelles ont les mêmes propriétés que les puissances entières.

Pour les puissances non rationelles :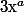

(x>0 fixé) on peut considérer une suite de quotients

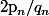qui tend vers

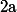et montrer que la suite

converge vers un réel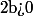

qui ne dépend pas de la suite, mais seulement de

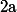. On défini alors

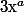comme étant égal à

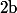et on démontre que les propriétés sont (encore) les mêmes que celle des puissances entières.

Une m'éthode plus simple consiste à définir (avec des primitives ou des solutions d'équa-diff) les fonction logaritme népérien et exponentielle puis de poser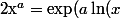

. On prouve que cette définition donne bien les propriétés espérées (celle des puissances entières) et, surtout, que si a est entier naturel, on trouve bien la même chose que le "bébète"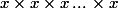

(heureusement !!!)

P.S. : Logo de LaTex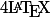

= \LaTeX (attention aux majuscules/minuscules)

par **Anonyme** » 09 Fév 2010, 11:07

On apprend tout cela a quel niveau ? TS? Sup ?

Merci encore une fois Ben.

par **Ben314** » 09 Fév 2010, 11:41

Je sais pas trop...
Le log et exp doivent être niveau 1ère ou Term (il me semble)
La notation x^(1/2) pour la racine carrée de x risque d'être vue avant (seconde ???)
Le fait de pouvoir calculer x^a avec a réel en approchant a par des quotients (c'est à dire sans utiliser le log et l'exponentielle) n'est à mon avis pas vu au lycée : il faut dire que c'est un peu compliqué pour montrer que la limite existe sans utiliser ni log, ni exponentielle !!!

Un "plus compétent que moi" confirmera ou infirmera mes dires...

Demonstration a^0 = 1 (a non nul)

Demonstration a^0 = 1 (a non nul)

Qui est en ligne