Je suis une quiche en analyse complexe, néanmoins, j'aimerais comprendre clairement la chose suivante :
Si on prend la fonction sinus sur le plan complexe à valeurs complexes :
Merci d'avance. :happy3:
barbu23 a écrit:Bonjour à tous,
Je suis une quiche en analyse complexe, néanmoins, j'aimerais comprendre clairement la chose suivante :
Si on prend la fonction sinus sur le plan complexe à valeurs complexes :, on me dit souvent que cette fonction, comme le cosinus aussi ( je ne sais pas si c'est aussi pour le tangent ) n'admet pas un inverse globale à droite, mais des inverses locaux à droite. Autrement dit, Il n'existe aucun
sur tout le corps complexe tel que :
, mais simplement une suite de fonctions sur des domaines
:
tel que :
. Pourriez vous m'expliquer clairement quels sont ces
et ces
? Pouvez vous me proposer une simple démonstration qui illustre ce fait ? Et pourquoi les
ne se recollent pas sur les
pour donner un présumé
?
Merci d'avance. :happy3:
Pythales a écrit:Soit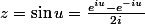
On en tire facilement)
Comme le log est défini àprès, les fonctions
correspondent à ces déterminations.
emdro a écrit: ... La fonctionest surjective. Par conséquent elle est bel et bien inversible à droite, i.e. il existe une fonction
telle que
.
barbu23 a écrit:Merci à vous deux. :happy3:
Et comment déterminer les?
Merci d'avance. :happy3:
emdro a écrit:... Je te laisse chercher comment se comporte la fonction sinus complexe. L'idéal serait que tu trouves toi-même un chemin trop grand qui te ramène à ton point de départ avec une discontinuité. Tu sentiras alors la nécessité d'imposer une limite du domaine de ta réciproque.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :