Le sinus en analyse complexe.
Bonsoir à tous,
Je me permets de relancer la discussion sur le sujet original de ce fil à propos des inverses à droites du sinus complexe :
Voici ce que j'avais envie de dire, mais que je n'arrivais pas à exprimer clairement la première fois :
Si vous jetez un il par ici : http://serge.mehl.free.fr/anx/surface_R.html , vous allez voir que les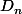 représentent les feuillets de la surface de Riemann sur laquelle sont définies les inverses à droite de la fonction sinus complexe, et qui a comme coupure une demi droite d'origine :
représentent les feuillets de la surface de Riemann sur laquelle sont définies les inverses à droite de la fonction sinus complexe, et qui a comme coupure une demi droite d'origine :  , et comme point de branchement : l'origine :
, et comme point de branchement : l'origine :  ( Vous lisez à l'intérieur de ce lien çi - dessus pour comprendre de quoi je parle ).
( Vous lisez à l'intérieur de ce lien çi - dessus pour comprendre de quoi je parle ).
Ma question est donc de savoir à quel inverse à droite correspond le feuillet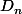 de la surface de Riemmann, est ce que ce sont les déterminations ? Comment sexpriment -elles en tant que fonctions uniformes et non multiformes ?
de la surface de Riemmann, est ce que ce sont les déterminations ? Comment sexpriment -elles en tant que fonctions uniformes et non multiformes ?
Merci d'avance. :happy3:
Je me permets de relancer la discussion sur le sujet original de ce fil à propos des inverses à droites du sinus complexe :
Voici ce que j'avais envie de dire, mais que je n'arrivais pas à exprimer clairement la première fois :
Si vous jetez un il par ici : http://serge.mehl.free.fr/anx/surface_R.html , vous allez voir que les
Ma question est donc de savoir à quel inverse à droite correspond le feuillet
Merci d'avance. :happy3:
Ben314 a écrit:Je ne vois pas où il "inverse" la fonction sinus dans ton papier (il inverse la fonction exponentielle)
C'est pareil, il suffit de remplacer le sinus par l'exponentielle. :happy3:
Les surfaces de Riemann s'appliquent à toutes sortes de fonctions complexes si j'ai bien compris ce qu'il y'a sur la page de ce lien que je t'ai mis dans le poste précedent. :happy3:
Bonjour à tous, :happy3:
On cherche à définir la racine carré complexe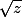 , sur un petit ouvert
, sur un petit ouvert  , par exemple un disque. On posera :
, par exemple un disque. On posera :
 = \{ \ f : U \to \mathbb{C} \ / \ f \ \text{est continue et} \ \forall z \in U \ : \ (f(z))^2 = z \ \})
Questions :
- Pourquoi : = \emptyset)
- Soit donc : non vide et connexe :
non vide et connexe :
Si :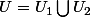 , les ouverts
, les ouverts  et
et 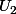 sont disjoints, pourquoi l'application :
sont disjoints, pourquoi l'application :  \to \mathcal{F} ( U_1 ) \times \mathcal{F} ( U_2 )) qui à
qui à  associe
associe ) est une bijection ?
est une bijection ?
Merci d'avance. :happy3:
On cherche à définir la racine carré complexe
Questions :
- Pourquoi :
- Soit donc :
Si :
Merci d'avance. :happy3:
barbu23 a écrit:Bonjour à tous, :happy3:
On cherche à définir la racine carré complexe, sur un petit ouvert
, par exemple un disque. On posera :
Questions :
- Pourquoi :
- Soit donc :non vide :
Si :, les ouverts
et
sont disjoints, pourquoi l'application :
qui à
associe
est une bijection ?
Merci d'avance. :happy3:
Salut,
pour ta première question, as-tu regardé ce que donne un relèvement de
Pour la deuxième, il faut peut-être juste bien l'écrire.
Pour la deuxième, ça me semble totalement évident : vu que U_1 et U_2 sont disjoint deux fonctions holomorphes sur U1 et U2 définissent à elle deux une fonction holomorphe sur U1uU2 et vice versa (sans aucune condition sur les fonctions)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Pour la deuxième, ça me semble totalement évident : vu que U_1 et U_2 sont disjoint deux fonctions holomorphes sur U1 et U2 définissent à elle deux une fonction holomorphe sur U1uU2 et vice versa (sans aucune condition sur les fonctions)
Il ne se passa rien sur la frontière qui sépare
barbu23 a écrit:Il ne se passa rien sur la frontière qui séparede
? Il se peut que :
n'est pas continue sur cette frontière. En plus, il faut utiliser le fait que :
qui est une condition qui définit
. ( Tu ne l'as pas utilisé ici à mon avis ). :happy3:
Ben si
As-tu écris ta preuve, il n'y a rien de diffcile. Où as-tu besoin de travailler sur la frontière? On ne parle pas de prolonger f, mais d'établir une bijection
Cette condition là ne risque pas de poser problème : c'est une condition ponctuelle donc si elle est vrai sur A (absolument quelconque) et sur B (tout aussi quelconque) elle sera évidement vrai sur la réunion des deux (et réciproquement)barbu23 a écrit:En plus, il faut utiliser le fait que :qui est une condition qui définit
. ( Tu ne l'as pas utilisé ici à mon avis ). :happy3:
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bonjour, :happy3:
Pour la bijection :
- Injectivité :
Soient :,(h_1,h_2) \in \mathcal{F} ( U_1 ) \times \mathcal{F} ( U_2 )) tel que :
tel que :  = ( h_1 , h_2 )) , alors
, alors  et
et  .
.
On pose : = \begin{cases} g_{1} (x) \ \ \mathrm{si} \ \ x \in U_1 \\ g_2 (x) \ \ \mathrm{si} \ \ x \in U_2 \end{cases}) et
et  = \begin{cases} h_{1} (x) \ \ \mathrm{si} \ \ x \in U_1 \\ h_2 (x) \ \ \mathrm{si} \ \ x \in U_2 \end{cases}) , Par conséquent :
, Par conséquent :  = h(x)) sur
sur  , d'où linjectivité, non ?
, d'où linjectivité, non ?
- Surjectivité :
Soit : \in \mathcal{F} ( U_1 ) \times \mathcal{F} ( U_2 )) , alors il existe
, alors il existe ) tel que :
tel que :  = ( g_1 , g_2 )) , il suffit de prendre :
, il suffit de prendre :  = \begin{cases} g_{1} (x) \ \ \mathrm{si} \ \ x \in U_1 \\ g_2 (x) \ \ \mathrm{si} \ \ x \in U_2 \end{cases}) , d'où la surjectivité, non ?
, d'où la surjectivité, non ?
Merci d'avance. :happy3:
Edit : J'ai corrgé :
- Injectivité :
Soient :) tels que :
tels que :  = \mathcal{F} ( h )) , cela implique que :
, cela implique que : ,(h_1,h_2) \in \mathcal{F} ( U_1 ) \times \mathcal{F} ( U_2 )) tel que :
tel que :  = ( h_1 , h_2 )) , alors
, alors  et
et  .
.
On pose : = \begin{cases} g_{1} (x) \ \ \mathrm{si} \ \ x \in U_1 \\ g_2 (x) \ \ \mathrm{si} \ \ x \in U_2 \end{cases}) et
et  = \begin{cases} h_{1} (x) \ \ \mathrm{si} \ \ x \in U_1 \\ h_2 (x) \ \ \mathrm{si} \ \ x \in U_2 \end{cases}) , Par conséquent :
, Par conséquent :  = h(x)) sur
sur  , d'où linjectivité, non ?
, d'où linjectivité, non ?
Pour la bijection :
- Injectivité :
Soient :
On pose :
- Surjectivité :
Soit :
Merci d'avance. :happy3:
Edit : J'ai corrgé :
- Injectivité :
Soient :
On pose :
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 144 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
