Lorsqu'on trigonalise une matrice A, on essaie d'obtenir une forme de Jordan.
On choisit à un moment une famille de vecteurs e(1) .....e(i)... e(n) définis par e(i-1)= (A-xI).e(i) où x est une valeur propre multiple de A. (J'espère que celui qui lit ça me comprend).
Je ne pige toujours pas pourquoi cette famille de vecteurs est une base de Ker[(A-xI)^n]...
Si quelqu'un peut m'expliquer...
Merci
(cours de maths prépa PSI)
Question bête sur la trigonalisation
8 messages
- Page 1 sur 1
D'abord la trigonalisation n'est pas au programme de la MPSI mais de la MP et de plus la forme de Jordan est hors programme. Ce résultat provient du lemme des noyaux qui indique que l'espace vectoriel est somme direct des sous espaces propres associés aux valeurs propres du spectre de l'endomorphisme considéré. La forme de Jordan est une méthode pour trigonaliser une matrice et la démonstration n'a rien de très technique (récurrence).
Je vais tente d'expliqué comment fonctionne la trigonalisation.
Prenons une matrice A appartenant a Mn(K) dont le polynome minimal est scindé(sinon ce n'est pas trigonalisable).
Le polynome minimal peut alors s'ecrire.
=(X-\lambda_{1})^{\alpha_{1}} \times \ldots \times (X-\lambda_{n})^{\alpha_{n}}) .
.
Comme on a P(A)=0 et que les polynomes^{\alpha_{i}}) sont premier entre eux deux à deux. Le lemme des noyaux nous dit que
sont premier entre eux deux à deux. Le lemme des noyaux nous dit que
^{\alpha_{1}}) \oplus \ldots \oplus ker((A-\lambda_{n}Id)^{\alpha_{n}}))
On notera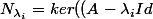^{\alpha_{i})) le sous espace caracteristique associé a la valeur propre
le sous espace caracteristique associé a la valeur propre 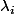
Ces sous espaces sont stables par A.
On sait alors que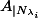 est trigonalisable.(polynome minimal divise le polynome minimal de A donc scindé CQFD)
est trigonalisable.(polynome minimal divise le polynome minimal de A donc scindé CQFD)
On alors mis la matrice sous forme d'une matrice diagonale par bloc,chaque bloc etant triangulaire.
Par ailleur chaque bloc peut s'ecrire sous la forme D+N.
D etant diagonalisable et N nilpotent.
Pour expliquer la reduction de Jordan, il suffit alors de se consacrer aux endomorphisme nilpotent.
On rajoutera le D apres...
Soit alors u, un endomorphisme nilpotent d'indice r.
cela signifie que pour tout x de E,=0)
alors pour tout x tels que\neq 0) .
.
La famille,u^{2}(x),\ldots,u^{r-1}(x))) est libre.
est libre.
Pour le montrer, tu peux le faire par récurrence:
tu prend une combinaison linaire nulle.
et tu montre que si les i premiers scalaires sont nuls alors le i+1 eme aussi.
initialisation : applique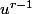 et tu obtiendra que le premier est nul.
et tu obtiendra que le premier est nul.
heredite: applique la bonne puissance de u
Ensuite,
si u est nilpotent d'indice r.
Les inclusions
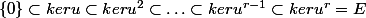 sont strcites (aucun ne sont egales)
sont strcites (aucun ne sont egales)
On peut alors montrer qu'il existe des sous espaces vectoriels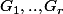 qui vérifient.
qui vérifient.
1)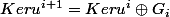
2) \subset G_{i-1})
3)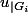 est injectif
est injectif
Cela se montre par récurrence décroissante mais un petit eu long...., j'ai la flemme
Une fois que l'on a cela on peut montrer grace a l'injectivite de u sur Gi qu'une famille libre de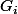 sera libre dans
sera libre dans 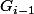
Ainsi, en écrivant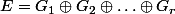
On prend une base) de
de 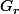 .
.
on obtient alors en appliquant u , une famille libre,\ldots,u(e_{r,p_{r}}))) que l'on complete en une base de
que l'on complete en une base de 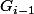 .
.
et ainsi de suite on applique u on obtient un truc libre dans Gr-2 on compelete etc....
On obtient une base de E, en reorganisant les vecteurs correctement,
on obtient un base dans laquelle la matrice est sous forme de bloc de jordan a diagonale nulle(car la matrice est nilpotente)
faudrait faire une immense matrice en Tex pour expliquer, si quelqu'un d'autre peut le faire, je maitrise pas tellement l'ecriture des matrices.....
Revenons maintenant à un endomorphisme trigonalisabe, on le met sous forme diagonale par bloc triangulaire.
On decompose chaque bloc en D+N.
(le D est la diagonale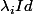 , le N le reste (triangulaire a diagonale nulle)
, le N le reste (triangulaire a diagonale nulle)
On sait qu'on peut mettre N sous forme de bloc de jordan a diagonale nulle (ce que j'ai essaye d'explique au dessus).
on rajoute le D
on fait comme sa avec tous les blocs et on a notre reduite de Jordan.
En esperant avoir été le plus clair possible et t'avoir aidé
Prenons une matrice A appartenant a Mn(K) dont le polynome minimal est scindé(sinon ce n'est pas trigonalisable).
Le polynome minimal peut alors s'ecrire.
Comme on a P(A)=0 et que les polynomes
On notera
Ces sous espaces sont stables par A.
On sait alors que
On alors mis la matrice sous forme d'une matrice diagonale par bloc,chaque bloc etant triangulaire.
Par ailleur chaque bloc peut s'ecrire sous la forme D+N.
D etant diagonalisable et N nilpotent.
Pour expliquer la reduction de Jordan, il suffit alors de se consacrer aux endomorphisme nilpotent.
On rajoutera le D apres...
Soit alors u, un endomorphisme nilpotent d'indice r.
cela signifie que pour tout x de E,
alors pour tout x tels que
La famille
Pour le montrer, tu peux le faire par récurrence:
tu prend une combinaison linaire nulle.
et tu montre que si les i premiers scalaires sont nuls alors le i+1 eme aussi.
initialisation : applique
heredite: applique la bonne puissance de u
Ensuite,
si u est nilpotent d'indice r.
Les inclusions
On peut alors montrer qu'il existe des sous espaces vectoriels
1)
2)
3)
Cela se montre par récurrence décroissante mais un petit eu long...., j'ai la flemme
Une fois que l'on a cela on peut montrer grace a l'injectivite de u sur Gi qu'une famille libre de
Ainsi, en écrivant
On prend une base
on obtient alors en appliquant u , une famille libre
et ainsi de suite on applique u on obtient un truc libre dans Gr-2 on compelete etc....
On obtient une base de E, en reorganisant les vecteurs correctement,
on obtient un base dans laquelle la matrice est sous forme de bloc de jordan a diagonale nulle(car la matrice est nilpotente)
faudrait faire une immense matrice en Tex pour expliquer, si quelqu'un d'autre peut le faire, je maitrise pas tellement l'ecriture des matrices.....
Revenons maintenant à un endomorphisme trigonalisabe, on le met sous forme diagonale par bloc triangulaire.
On decompose chaque bloc en D+N.
(le D est la diagonale
On sait qu'on peut mettre N sous forme de bloc de jordan a diagonale nulle (ce que j'ai essaye d'explique au dessus).
on rajoute le D
on fait comme sa avec tous les blocs et on a notre reduite de Jordan.
En esperant avoir été le plus clair possible et t'avoir aidé
Je v essaye de faire un dessin comme je pe pour expliquer lorganisation de la base.
on a donc E comme somme directe des Gi ( designera une injection)
designera une injection)
&\rightarrow&\ldots&\rightarrow& u^{r-1}(e_{r,1}) \\<br />e_{r,2}&\rightarrow&u(e_{r,2}) &\rightarrow&\ldots&\rightarrow&u^{r-1}(e_{r,2})\\ <br />\vdots&&\vdots&&\vdots&&\vdots\\<br />e_{r,p_{r}}&\rightarrow &u(e_{r,p_{r}})&\rightarrow&\ldots&\rightarrow&u^{r-1}(e_{r,p_{r}})\\ <br />&&e_{r-1,1}&\rightarrow& \ldots&\rightarrow&u^{r-2}(e_{r-1,1}) \\<br />&&\vdots&&\vdots&&\vdots\\<br />&&e_{r-1,p_{r-1}}&\rightarrow&\ldots&\rightarrow&u^{r-2}(e_{r-1,p_{r-1}}) \\<br />&&&&&&\vdots\\<br />\end{array})
on notera Bi la famille forme des vecteurs de la ligne i pri de la droite vers la gauche
alors, la matrice de u dans la base (B1,B2,...,Bn) est de la forme voulu.
en effet, les B1,..,Bn sont stables (c tres mal dit d'accord)
et chaque Bi nous donne un bloc de jordan(assez facil a voir)
Voila si quelque veut completer cette explication
on a donc E comme somme directe des Gi (
on notera Bi la famille forme des vecteurs de la ligne i pri de la droite vers la gauche
alors, la matrice de u dans la base (B1,B2,...,Bn) est de la forme voulu.
en effet, les B1,..,Bn sont stables (c tres mal dit d'accord)
et chaque Bi nous donne un bloc de jordan(assez facil a voir)
Voila si quelque veut completer cette explication
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
