[MPSI] petite question toute bete sur changement de base

[guigui777]

On pourrait repartir du début, la je comprends plus rien ! :hum: :mur:

Que dois-je faire avec ma matrice A ?
Dois-je exprimer ... ?

mon avis c'est que tu dois trouver ta base. Puis ensuite tu dois te servir de A et de la base pour trouver mat(f)

[pouik]

mon avis c'est que tu dois trouver ta base.

De quelle base s'agit-il ?
Dois-je la déterminer avec les .. et si oui, comment ?

[Joker62]

Soit avec est le vecteur de ayant un 1 sur la i_ème composante et 0 autre part.

Bon en gros B c'est la base canonique de R^3.
Je suppose que ici A représente LA matrice de f DANS la base canonique.

On a

Soit

Qui représente la matrice de passage de la base B vers la base

Un calcul rapide nous donne l'inverse de P ( surtout grâce à [url="http://wims.unice.fr/wims/"]http://wims.unice.fr/wims/[/url] )



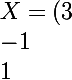On pose le premier vecteur colonne de A

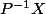
Alors ici, X est exprimé dans la base B, et en calculant on trouvera le vecteur X dans la base B'

Fait pareil avec les autres vecteurs colonnes, tu auras la nouvelle matrice DANS la base B'