Bonjour, j'ai un problème que j'aimerais bien résoudre mais il est long et j'ai un peu de mal à le faire, voici l'énoncé :
ProblèmeOn note
)
le

-espace vectoriel des fonctions réelles de classe

sur

.
On considère trois fonction
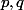
et

de cet espace vectoriel définies pour
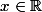
par
=e^{x} })
=e^{2x}})
=e^{x^2}})
On note
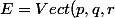)
l'espace vectoriel engendré par la famille
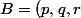)
.
Partie 11) Soit

et

trois réels tel que
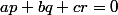
. En utilisant les comportements relatifs des fonctions p,q et r en

, montrer que nécessairement,
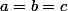
.
2) Que peut-on en conclure sur

pour

? Quelle est la dimension de

?
Partie 2 3) Si
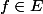
;
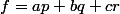
avec
\in \mathbb{R^3})
, exprimier a,b,c en fonction de
,f'(0))
et
)
. ( on résoudra un système 3x3 ).
4) On note

l'application de

dans
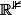
qui, à toute fonction
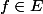
associe le triplet
,f'(0),f(1)))
.
Montrer que

est un isomorphisme de

sur
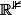
.
et puis après il y a une partie 3, mais je vais sans doute la faire plus tard...
1) Pour moi, c'est évident que pour que
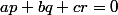
, il faut nécessairement que
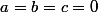
, mais je ne vois pas comment utiliser les comportement de p,q et r en

car ces trois fonctions tendent ont une limite infinie en

...
2) eh bien si
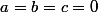
, alors

est une famille libre dans

, mais la dimension....
3)alors j'ai calculé:
=a+b+c)
=a+2b)
=ae+be^2+ce)
et j'ai trouvé les solutions du système 3x3...
4) j'ai pas encore trouvé...
Pourriez vous m'aider ?
