Décomposé un entier
Olympiades mathématiques, énigmes et défis
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 07 Mai 2007, 12:00
par mt2sr » 07 Mai 2007, 12:00
bonjour
soit n un entier naturel
montrer qu'il existe un unique couple d'enties naturels (t,k) tel que
n=t²+k avec 0<=k<=2t
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 07 Mai 2007, 15:47
par fahr451 » 07 Mai 2007, 15:47
bonjour
je doute que cette question soit dans la bonne rubrique
n est compris entre deux carrés consécutifs
il existe un unique t naturel /
t^2 =< n < (t+1)^2 on pose k = n - t^2 on a
0=< k< (t+1)^2 -t^2 = 2t +1 et l'existence ; l'unicité est claire
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 07 Mai 2007, 17:23
par fahr451 » 07 Mai 2007, 17:23
ben oui je corrige merci bien
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 07 Mai 2007, 22:31
par mt2sr » 07 Mai 2007, 22:31
la question est simple il s'agit d'une décompsition d'un entier que j'ai employé pour répondre à l'exercice voici son énoncé:
soit
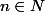
calculer
)
E(x) désigne la partie entière de x
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 08 Mai 2007, 14:44
par mt2sr » 08 Mai 2007, 14:44
bonjour
est-ce que vous avez une réponse à cet exercice?
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 09 Mai 2007, 18:17
par mt2sr » 09 Mai 2007, 18:17
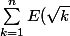=nE(\sqr{n})+\frac{E(\sqr{n})(1-E(\sqr{n}))(5+2E(\sqr{n}))}{6})
j'espère que j'ai pas comi des érreurs
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 09 Mai 2007, 19:47
par yos » 09 Mai 2007, 19:47
Le résultat a l'air juste. C'est pas mal. Je l'avais calculé pour n=p²-1 uniquement.
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 10 Mai 2007, 08:45
par mt2sr » 10 Mai 2007, 08:45
bonjour
vous avez une dem pour le cas général
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 10 Mai 2007, 17:25
par yos » 10 Mai 2007, 17:25
On doit pouvoir faire ça par récurrence. On a
=E(\sqrt{n+1}))
sauf si n=p²-1. Il s'agit donc de distinguer deux cas.
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 11 Mai 2007, 12:36
par mt2sr » 11 Mai 2007, 12:36
bonjour
il s'agit de calculer et non montrer l'égalité
j'ai procédé sans étude des cas
votre démarche m'interesse pouviez-vous donner une dem détaillé
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 11 Mai 2007, 15:08
par Imod » 11 Mai 2007, 15:08
Bonjour à tous les 2 , rien de mystérieux dans cette formule mais un peu de calcul .
Pour n entier donné , je note

, pour

et
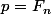
.

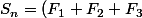+(F_4+F_5+F_6+F_7+F_8)+(F_9+F_{10}+...+F_{15})+...+(F_{p^2}+...+F_{p^2+q)})
Avec
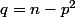
et

.
Comme pour
^2)
,
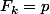
:
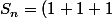+(2+2+2+2+2)+(3+...+3)+...+(p+...+p))
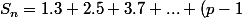.(2p+1)+p.(q+1))
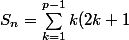}+p(q+1)})
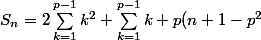})
Il n'y a plus qu'à appliquer les formules donnant
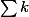
et

pour obtenir :
(2p+5)}{6})
Imod
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 12 Mai 2007, 09:50
par mt2sr » 12 Mai 2007, 09:50
bravo imod
c'est la méthode que j'ai utilisé
je vous propose un autre exercice
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 12 Mai 2007, 10:03
par Flodelarab » 12 Mai 2007, 10:03
Quel rapport entre le titre et le problème résolu ?
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 12 Mai 2007, 11:07
par mt2sr » 12 Mai 2007, 11:07
calculer la somme est une application de la décomposition n=t²+k 0<=k<=2t
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
