Montrer qu'un nombre est un entier
Olympiades mathématiques, énigmes et défis
-
Mukito
- Membre Naturel
- Messages: 64
- Enregistré le: 19 Oct 2008, 11:50
-
 par Mukito » 27 Déc 2010, 14:09
par Mukito » 27 Déc 2010, 14:09
Bonjour , voila le nombre:
(2 + racine(5) ) ^ (1/3) + (2 - racine(5) ) ^ (1/3)
Comme vous l'aurez compris, il faut montrer que c'est un entier.
Cette question se trouve dans un contexte d'identité remarquable.
Merci de bien vouloir répondre :we:
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 27 Déc 2010, 14:18
par windows7 » 27 Déc 2010, 14:18
salut,
on pourrait bien le mettre au cube et tombé sur 64, ce qui prouverait, à condition que le nombre soit reel, que c'est 4 ..
-
Mukito
- Membre Naturel
- Messages: 64
- Enregistré le: 19 Oct 2008, 11:50
-
 par Mukito » 27 Déc 2010, 14:31
par Mukito » 27 Déc 2010, 14:31
Je sais pas comment tu trouves 64.
normalement, le tout au cube, on devrait voir des puissances 2/3 qui se baladent :ptdr:
De tout façon, je sais que cet entier est 1 et non 4.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 27 Déc 2010, 14:43
par girdav » 27 Déc 2010, 14:43
En notant

le nombre en question on trouve que
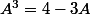
et la seule racine réelle de
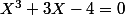
est

.
-
Mukito
- Membre Naturel
- Messages: 64
- Enregistré le: 19 Oct 2008, 11:50
-
 par Mukito » 27 Déc 2010, 14:56
par Mukito » 27 Déc 2010, 14:56
Effectivement on trouve comme racine 1 et 2 autres racines complexes : -1/2(1-i rac15) et -1/2(1+i rac 15).
Donc ce nombre est bien un entier.
Merci bien! :lol3:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 27 Déc 2010, 17:19
par Zweig » 27 Déc 2010, 17:19
Salut,
En posant
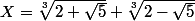
, on a alors :
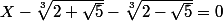
et donc (*)
^3 - \left(\sqrt[3]{2-\sqrt{5}}\right)^3 = 3X \left(\sqrt[3]{2+\sqrt{5}}\right) \left(\sqrt[3]{2-\sqrt{5}}\right))
Il nous reste alors à résoudre :
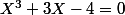
1 est clairement racine et par factorisation, on montre que c'est la seule racine réelle, d'où le résultat
(*) Pour tout triplet de réels :
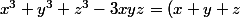(x^2 + y^2 + z^2 - xy - xz - yz))
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 27 Déc 2010, 21:45
par windows7 » 27 Déc 2010, 21:45
windows7 a écrit:salut,
on pourrait bien le mettre au cube et tombé sur 64, ce qui prouverait, à condition que le nombre soit reel, que c'est 4 ..
mdr j'ai totalement bugger !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
