Sommes (2)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Anonyme
 par Anonyme » 21 Déc 2012, 18:37
par Anonyme » 21 Déc 2012, 18:37
Kikoo
Surtout essaie de passer de bonnes fêtes
et évite de trop réfléchir car les vacances c'est pas fait pour ça !
-
Anonyme
 par Anonyme » 28 Déc 2012, 11:22
par Anonyme » 28 Déc 2012, 11:22
un petit UP comme on dit.....
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 28 Déc 2012, 12:30
par adrien69 » 28 Déc 2012, 12:30
Ben quelle est la question ?
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 28 Déc 2012, 17:01
par adrien69 » 28 Déc 2012, 17:01
Bah pour le lien que tu as mis, déjà il y a une bourde, S_2n vaut toujours 1 pas 0.
Et pour la formule d'Euler (qui normalement n'est pas celle-ci mais passons), astuce terrible :
On pose u_n=H_n -ln(n) et v_n=u_n -1/n
Montrer que ces deux suites sont adjacentes ;) :ruse:
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 28 Déc 2012, 17:03
par adrien69 » 28 Déc 2012, 17:03
Ah pour l'exercice que j'ai posé il est vraiment facile en fait quand tu le prends bien :D
Faut faire un dessin et pis c'est fini :bad3:
-
Anonyme
 par Anonyme » 28 Déc 2012, 17:17
par Anonyme » 28 Déc 2012, 17:17
adrien69 a écrit:Bah pour le lien que tu as mis, déjà il y a une bourde, S_2n vaut toujours 1 pas 0.
Je ne comprends pas ton message ?
Si
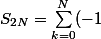^{2k}+(-1)^{2k+1})
avec N=0 : on obtient
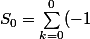^{2k}+(-1)^{2k+1}=(-1)^{0}+(-1)^{1}=1-1=0)
avec N=1 : on obtient
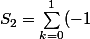^{2k}+(-1)^{2k+1}=(-1)^{0}+(-1)^{1}+(-1)^{2}+(-1)^{3}=1-1+1-1=0)
..etc...
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 28 Déc 2012, 17:28
par adrien69 » 28 Déc 2012, 17:28
ptitnoir a écrit:Je ne comprends pas ton message ?
Si
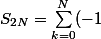^{2k}+(-1)^{2k+1})
avec N=0 : on obtient
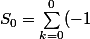^{2k}+(-1)^{2k+1}=(-1)^{0}+(-1)^{1}=1-1=0)
avec N=1 : on obtient
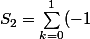^{2k}+(-1)^{2k+1}=(-1)^{0}+(-1)^{1}+(-1)^{2}+(-1)^{3}=1-1+1-1=0)
..etc...
C'est au tout début que tu te trompes en fait.
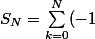^{k})
On est d'accord ? Donc on a
Pour N>1
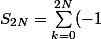^{k}=\sum_{0\le 2k \le 2N}(-1)^{2k} +\sum_{0 \le 2k+1 \le 2N}(-1)^{2k+1} = \sum_{0 \le 2k \le 2N}1 - \sum_{0 \le 2k+1 \le 2N}1)
pour la somme de gauche k est compris entre 0 et N, on a donc N+1 fois le terme 1
pour la somme de droite k est compris entre 0 et N-1, on a donc N fois le terme 1
La différence des deux est donc 1
On en déduit le résultat pour N>1 et si N=0 eh bien la somme So vaut (-1)°=1
Voili voilou !
-
Anonyme
 par Anonyme » 28 Déc 2012, 18:09
par Anonyme » 28 Déc 2012, 18:09
@adrien69
NON je ne suis pas d'accord avec tes explications car comme cette série n'est ni à termes positifs , ni ne converge :
DONC on ne peut pas écrire que :
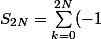^{k}=\sum_{0\le 2k \le 2N}(-1)^{2k} +\sum_{0 \le 2k+1 \le 2N}(-1)^{2k+1})
et c'est la raison pourquoi j'ai raisonné à partir de la somme
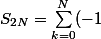^{2k}+(-1)^{2k+1})
au lieu de la somme
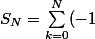^{k})
La problématique de cet
"speudo exo" est
- qu'on sait que la série
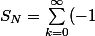^{k})
diverge
"grosiérement"- alors que

on a
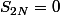
Et cet exo demande de justifier et d'expliquer POURquoi ;;;;
ps)Si tu ne comprends pas ce que je veux dire : voici un énoncé plus facile à comprendre qui
"retranscrit" la même question :
ptitnoir a écrit:@Kikoo
D'après le message précédent de le_chat :
on sait que la série 1 -1 +1 -1 +1 -1 .....etc.......... ne converge pas
Pourtant on a 1 -1 +1 -1 +1 -1 .....etc.......... = (1 -1) + (1 -1) + (1 -1) .....etc.......... =0
Chercher l'erreur (en essayant de justifier) ?
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 28 Déc 2012, 18:26
par adrien69 » 28 Déc 2012, 18:26
Aah okayy. Je pensais que tu travaillais avec une suite extraite, pas que tu faisais de la sommation par paquets (c'est pas comme ça qu'on note habituellement)
Mea culpa. Mea maxima culpa.
-
Anonyme
 par Anonyme » 28 Déc 2012, 18:40
par Anonyme » 28 Déc 2012, 18:40
@adrien69
Comment aurais tu énoncé cette question ?
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 28 Déc 2012, 19:22
par adrien69 » 28 Déc 2012, 19:22
Euh, attends, attends...
J'ai travaillé sur les sommes partielles donc j'avais bien le droit d'écrire ce qui précède. On se fout du signe pour ça. J'expliquerai plus en détail quand je serai sur mon pc.
Edit :
En fait tu as tout à fait le droit de considérer ta somme à double terme, mais pas celui de l'appeler

qui est exactement ce que moi j'ai calculé.
Et c'est en fait comme ça qu'on fait de la sommation par paquet :
Ici tu poses
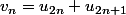
et tu poses
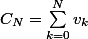
qui en fait ne vaut pas

comme tu semblais le croire, mais

Je ne sais pas trop si je suis clair en expliquant ça...
-
Anonyme
 par Anonyme » 29 Déc 2012, 10:13
par Anonyme » 29 Déc 2012, 10:13
@adrien69
Tu as raison , ma notation est ambigüe
car on peut croire que la suite de terme général

est une suite extraite de la suite
) (alors que dans mon esprit , il n'y avait pas de lien car je voulais uniquement montrer ce que donne un exemple de sommation par paquet
(alors que dans mon esprit , il n'y avait pas de lien car je voulais uniquement montrer ce que donne un exemple de sommation par paquet
et montrer un résultat surprenant
Remarque : On peut également "montrer" , si on fait un peu n'importe quoi avec cette série , que cette série tend vers +infini ( bien sûr avec un raisonnement faux et en prenant la série de terme général 
En conclusion : on peut quasiment "montrer" et dire TRES VITE "n'importe quoi" si on commence à vouloir faire des sommations par paquet.... ) ET je suis d'accord avec toi :
J'aurais du créer une autre série de terme général
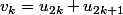
pour éviter cette ambigüité
Merci pour ces "commentaires avisés"
ps) Autre question:
Je sais que
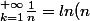+c+o(1))
avec
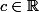
est le "début" du développement dit "asymptotique" de la série harmonique
mais je pensais aussi que cette formule était également appelée "formule d'Euler"
D'après toi : Où est le blem ?
-
Anonyme
 par Anonyme » 29 Déc 2012, 12:02
par Anonyme » 29 Déc 2012, 12:02
Kikoo <3 Bieber a écrit:Hello Ptitnoir,
Promis, je m'y colle demain après-midi (vacances !!!!).
@Kikoo
Promesse d'ivrogne...ps)Change de colle !

-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Déc 2012, 12:17
par Kikoo <3 Bieber » 29 Déc 2012, 12:17
Ouais ben je vois pas comment l'aborder :p
Une piste ?
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 29 Déc 2012, 12:18
par adrien69 » 29 Déc 2012, 12:18
@ptitnoir
Boarf aucune idée. Je pense juste que la formule d'Euler est le truc ultra connu

Et que les formules d'Euler étaient les expressions exponentielles des sinus (à moins que ça ce soit de de Moivre ?)
Tandis que le c qui intervient dans le développement asymptotique de la série harmonique est la constante d'Euler.
Après je pense que tu as le droit de dire que c'est que c'est une formule d'Euler. Mais ce malade en a trouvé tellement qu'on ne saurait pas de laquelle tu parles.
Jette un ptitcoupdoeil sur l'article wikipedia 'sommation par paquets' y a plein de théorèmes sympas dans cette théorie qui empêchent de dire des conneries en colle. Et le pb que j'avais posé est un peu en lien. Ça s'appelle le théorème de réarrangement de Weierstrass (je pense).
-
Anonyme
 par Anonyme » 29 Déc 2012, 12:31
par Anonyme » 29 Déc 2012, 12:31
@adrien69
OK , pigé
Suggestion :
Au lieu d'écrire
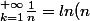+c+o(1))
avec
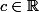
pourquoi ne pas écrire
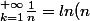+) p
p )
avec
p 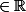
et appeler cette formule "formule de
ptitnoir" ?
ps)Si tu es d'accord , je vais publier ce résultat dans la presse dite
"scientifique" pour essayer d'obtenir la médaille "Fields" 2013 ?
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 29 Déc 2012, 12:37
par adrien69 » 29 Déc 2012, 12:37
La Fields n'est délivrée que tous les quatre ans, va falloir que tu attendes un peu avant de toucher ton million ;)
-
Anonyme
 par Anonyme » 29 Déc 2012, 12:52
par Anonyme » 29 Déc 2012, 12:52
Merde alors !
Bon ben... je vais plutôt continuer à jouer au loto !
ps1)
J'ai calculé les probas d'obtenir les 5 bons numéros + le n° complémentaire
Compte tenu de ces calculs : en faisant une martingale je suis sûr de gagner un jour
( sachant que si je meurs mes enfants ont pour "mission" de continuer cette martingale )
ps2)
Je suis TRES TRES riche
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 29 Déc 2012, 12:57
par adrien69 » 29 Déc 2012, 12:57
ptitnoir a écrit:Merde alors !
Bon ben... je vais plutôt continuer à jouer au loto !
ps1)
J'ai calculé les probas d'obtenir les 5 bons numéros + le n° complémentaire
Compte tenu de ces calculs : en faisant une martingale je suis sûr de gagner un jour
( sachant que si je meurs mes enfants ont pour "mission" de continuer cette martingale )
ps2)
Je suis TRES TRES riche
Une martingale au loto ? C'est quoi ton truc ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités