Sommes (2)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 19 Déc 2012, 22:40
par Kikoo <3 Bieber » 19 Déc 2012, 22:40
ptitnoir a écrit:Kikoo <3 Bieber
On a
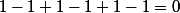
Est ce que la série
 .....etc..........
.....etc.......... converge ?
Je ne sais pas.
Dans le sens de Cesaro, il est clair qu'elle converge (vers 1/2) mais on ne peut sinon pas connaitre sa limite.
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 19 Déc 2012, 22:42
par Le_chat » 19 Déc 2012, 22:42
Non, pas dans le sens usuel, car pour qu'une série converge il faut que son terme général tende vers 0.
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 19 Déc 2012, 22:51
par Kikoo <3 Bieber » 19 Déc 2012, 22:51
J'en profite donc pour demander un peu d'aide !
J'aimerais montrer que la somme
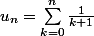
tend vers l'infini.
Pour cela, j'ai songé aux équivalents, mais sachant que je ne peux en sommer un nombre indéterminé, cela ne fonctionnera pas.
J'ai également pensé revenir à la définition : Montrer qu'à partir d'un certain rang, notre somme dépasse un réel fixé.
Une piste ?
Ou peut-être devrais-je étudier
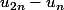
?
-
Anonyme
 par Anonyme » 19 Déc 2012, 22:59
par Anonyme » 19 Déc 2012, 22:59
@Kikoo
Connais tu la série harmonique ?
C'est un GRAND classique et il faut savoir démontrer que cette série diverge
et il y a plusieurs démos possibles
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 19 Déc 2012, 23:05
par Kikoo <3 Bieber » 19 Déc 2012, 23:05
Merci pour ta réponse ptitnoir :zen:
Oui, je connais cette série, et donc ? Pourrais-je la comparer avec l'autre ? Mais ce ne serait pas très utile, puisqu'on veut montrer qu'elle diverge or son terme général est inférieur en valeur absolue à celui de la série harmonique. Pourrais-tu développer stp ?
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 19 Déc 2012, 23:11
par Le_chat » 19 Déc 2012, 23:11
Là tu étudies précisément la série harmonique... Mais oui montrer que (u2n-un) ne tend pas vers 0 est une bonne idée.
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 19 Déc 2012, 23:20
par Kikoo <3 Bieber » 19 Déc 2012, 23:20
Ah mais oui, j'ai bien
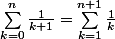
(je m'en étais pourtant persuadé hier soir avant d'aller me coucher et je réitère aujourd'hui la bêtise que j'avais trainée) !
Et donc je sais que
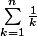
diverge d'où la conclusion ?

Si je veux montrer que la série harmonique diverge, j'utilise le fait que
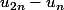
est supérieur à 1/2 pour tout n entier donc il est impossible que la suite converge.
Merci le_Chat !

)
-
Anonyme
 par Anonyme » 20 Déc 2012, 00:11
par Anonyme » 20 Déc 2012, 00:11
@Kikoo
Sais tu que
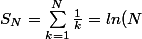)
-
Anonyme
 par Anonyme » 20 Déc 2012, 10:02
par Anonyme » 20 Déc 2012, 10:02
@Kikoo
Voici un autre exo sur la série harmonique ( qui est également un grand classique ) :
Démontrer que la suite
)
définie par
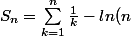)
converge
-
Anonyme
 par Anonyme » 20 Déc 2012, 10:22
par Anonyme » 20 Déc 2012, 10:22
@Kikoo
D'après le message précédent de
le_chat :
on sait que la série
 .....etc..........
.....etc.......... ne converge pas
Pourtant on a
 .....etc..........
.....etc.......... =
 + (1 -1) + (1 -1)) .....etc..........
.....etc.......... 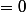 Chercher l'erreur (en essayant de justifier) ?
Chercher l'erreur (en essayant de justifier) ?
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 20 Déc 2012, 20:18
par Kikoo <3 Bieber » 20 Déc 2012, 20:18
Hello Ptitnoir,
Promis, je m'y colle demain après-midi (vacances !!!!).
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 20 Déc 2012, 20:25
par Skullkid » 20 Déc 2012, 20:25
Sans trop dévoiler l'erreur proposée par ptitnoir, qui est intéressante à trouver par soi-même, un conseil qui pourra servir : dès que tu vois des points de suspension dans un énoncé mathématique, ou que tu as envie d'en utiliser, ça doit automatiquement tirer la sonnette d'alarme. C'est pas forcément faux d'utiliser les points de suspension (quoique les puristes diront qu'on peut et qu'on devrait toujours s'en passer, puisque ce n'est pas un symbole proprement mathématique) mais il y a énormément d'occasions de mal les utiliser.
-
Anonyme
 par Anonyme » 20 Déc 2012, 20:51
par Anonyme » 20 Déc 2012, 20:51
Autre énoncé (qui est à mon avis plus difficile à comprendre....)D'après le message précédent de
Le_chat :
on sait que la série

de terme général est
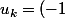^k)
ne converge pas et même diverge
"grossièrement"On peut démontrer que
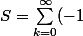^k)
n'existe pas
Cependant

on a S_
2N=
^{2k}+(-1)^{2k+1}=0)
Expliquer pourquoi la suite
)
ne converge pas vers 0 ?
(EDIT) pour correction en rouge suite au message de Le_chat qui suit ce message
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 20 Déc 2012, 20:53
par Le_chat » 20 Déc 2012, 20:53
ptitnoir a écrit:Cependant

on a
^{2k}+(-1)^{2k+1}=0)
Non, ça c'est (S_2n). Justement. Si on avait Sn=0 tout le temps, (Sn) serait convergente.
EDIT: Sinon concernant la limite de
^k}{k+1})
, il y a une preuve toute simple. On a:
^k}{k+1}=\sum_{k=0}^{n} \frac{1}{2k+1}-\sum_{k=1}^{n} \frac{1}{2k})
.
En notant (Hn) la série harmonique:
^k}{k+1}=H_{2n+1}-\sum_{k=1}^{n} \frac{1}{2k}-\sum_{k=1}^{n} \frac{1}{2k}=H_{2n+1}-H_n)
, d'où la limite, ln(2), sachant que
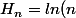+c+o(1))
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 20 Déc 2012, 20:57
par adrien69 » 20 Déc 2012, 20:57
ptitnoir a écrit:@Kikoo
D'après le message précédent de
le_chat :
on sait que la série
 .....etc..........
.....etc.......... ne converge pas
Pourtant on a
 .....etc..........
.....etc.......... =
 + (1 -1) + (1 -1)) .....etc..........
.....etc.......... 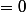 Chercher l'erreur (en essayant de justifier) ?
Chercher l'erreur (en essayant de justifier) ?
@ptitnoir, et qui aura envie de se creuser les méninges
Dans le même genre que ce que tu viens de donner,
Si on considère une suite (An) de réels, telle que la série associée soit semi-convergente (converge mais pas absolument), montrer que pour tout b fini ou infini, il existe une permutation s de N telle que la série associée à As(n) converge vers b.
Qu'en est-il si l'on considère des vecteurs de taille finie en guise de An ?
Good luck !

-
Anonyme
 par Anonyme » 20 Déc 2012, 21:10
par Anonyme » 20 Déc 2012, 21:10
@Le_chat
Faut il encore savoir démontrer que
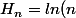+c+o(1))
?
A mon avis : cette formule , appelée formule D'Euler , n'est pas forcément connue par les tous les
"taupins et les taupines"
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 20 Déc 2012, 21:13
par Le_chat » 20 Déc 2012, 21:13
C'est certain, surtout en début de sup. Mais bon c'est la seule façon que j'ai trouvé pour éviter les sommes de Riemann.
-
Anonyme
 par Anonyme » 20 Déc 2012, 21:18
par Anonyme » 20 Déc 2012, 21:18
@Le_chat
On peut je pense y arriver
- par les séries entières
ou
- par des développements dits "asymptotiques"
-
Anonyme
 par Anonyme » 21 Déc 2012, 18:31
par Anonyme » 21 Déc 2012, 18:31
Kikoo <3 Bieber a écrit:Hello Ptitnoir,
Promis, je m'y colle demain après-midi (vacances !!!!).
Euh je pense que tu voulais dire demain soir car il est déjà 18H30.....
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 21 Déc 2012, 18:33
par Kikoo <3 Bieber » 21 Déc 2012, 18:33
Ouais ben ça va ptitnoir, j'y réfléchis, excuse-moi d'avoir autre chose à faire (c'est la fin du monde) ^^
T'inquiète je suis à l'oeuvre.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
.....etc.......... converge ?
.....etc.......... ne converge pas
.....etc.......... =
.....etc..........