Sommes (2)

[Kikoo <3 Bieber]

Salut

J'ai et deux suites à valeurs dans , telles que :
.

Il a falu que je montre que
Maintenant il faut que je montre que

J'ai commencé ainsi :

Et je vois bien que les coefficients concordent, mais je ne comprends pas la manière de passer de cette écriture à celle que l'on me demande.

Merci de bien vouloir m'aider un peu.

[Luc]

Salut,

tu as bien commencé! Ça serait bien d'utiliser la formule que tu as démontré précédemment, non?

[Kikoo <3 Bieber]

Salut Luc, je peux décidément te faire confiance ! :D

J'avais remarqué la correspondance des coefficients (binomiaux) mais je ne voyais pas comment les sortir d'une somme à l'autre, à moins d'effectuer un changement d'indices ?

[Luc]

Salut Luc, je peux décidément te faire confiance !

J'avais remarqué la correspondance des coefficients (binomiaux) mais je ne voyais pas comment les sortir d'une somme à l'autre, à moins d'effectuer un changement d'indices ?

et je te laisse continuer!

[Kikoo <3 Bieber]

Merci ! Suis-je bête, je viens de m'apercevoir qu'on pouvait le considérer comme un scalaire !

[Kikoo <3 Bieber]

Kikoo !

Je voulais juste m'assurer que ce que j'ai fait sur la somme suivante est suffisant :

[Luc]

Kikoo !

Je voulais juste m'assurer que ce que j'ai fait sur la somme suivante est suffisant :

Oui c'est bon.
Connais tu un équivalent simple de en l'infini (c'est a dire une suite telle que )?. Chercher un équivalent simple c'est quantifier a quelle vitesse Hn tend vers l'infini en l'infini.

[Kikoo <3 Bieber]

Oh oui, j'en connais un ^^

Nous avons alors je pense.

[Kikoo <3 Bieber]

Salut,

Je ne vois pas comment on passe de à
Je crois saisir pour le passage de la somme du début vers le premier membre mais pas le second membre : pourquoi impose-t-on i<j ?

[Luc]

[quote="Kikoo j}x_ix_j=\sum_{i\not = j}x_ix_j[/TEX]

[Kikoo <3 Bieber]

Salut,

en fait,

D'accord, je vois

Cela revient à dire : ?

[Luc]

[quote="Kikoo j}x_ix_j[/TEX] ?[/quote]
Oui, c'est ça. Ce qu'il y a dans la somme est symétrique en (i,j).

[Kikoo <3 Bieber]

Super, merci beaucoup Luc :)

[Kikoo <3 Bieber]

Yop,

Apès un DS, une somme me tracasse.

Je devais montrer que
[CENTER]
[/CENTER]

Bon, pas évident de me remémorer ce que j'ai fait mais il me semble que je suis parti comme ceci :


Puis après, brouillon dans ma tête (et je crois que je m'en suis arrêté là aussi sur la feuille).
Quelqu'un peut-il me proposer une issue ?

Merci d'avance

[Skullkid]

Salut, tu as fait le plus dur. La somme complexe vaut comme tu l'as écrit (inutile de te trimballer les parties réelles à chaque ligne, fais tes calculs sur la somme complexe et prends la partie réelle tout à la fin, ça te fera des parenthèses en moins et rendra le tout plus lisible).

Le souci c'est que (-i)^n c'est un coup réel, un coup imaginaire, donc finis le calcul de la somme complexe en distinguant selon la parité de n, puis prends la partie réelle. Ensuite la petite astuce c'est de regarder ce que donne selon la parité de n et ô miracle... Cette dernière étape sert surtout à présenter le résultat joliment, sans faire de distinction sur la parité de n.

[Kikoo <3 Bieber]

Salut, tu as fait le plus dur. La somme complexe vaut comme tu l'as écrit (inutile de te trimballer les parties réelles à chaque ligne, fais tes calculs sur la somme complexe et prends la partie réelle tout à la fin, ça te fera des parenthèses en moins et rendra le tout plus lisible).

Le souci c'est que (-i)^n c'est un coup réel, un coup imaginaire, donc finis le calcul de la somme complexe en distinguant selon la parité de n, puis prends la partie réelle. Ensuite la petite astuce c'est de regarder ce que donne selon la parité de n et ô miracle... Cette dernière étape sert surtout à présenter le résultat joliment, sans faire de distinction sur la parité de n.

Salut Skullkid et merci pour ta réponse !

Si n est multiple de 2, cela donne -1 un coup puis 1 un autre coup.
Si n est impair, cela donne -i ou i.

Je disjoins deux cas :

Si n est pair, alors on a
Donc la somme vaut
Si n est impair, on a
D'où la somme :

Et là, comme
Nous concluons.
C'est bon ?

[Kikoo <3 Bieber]

Je viens de m'apercevoir que i exposé à des puissances consécutives alterne ses signes donc mes "plus ou moins" sont faux je suppose ?

[Skullkid]

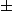
Ouais les c'est pas top, même s'il n'y avait pas cet effet d'alternance de signe modulo 4. Écris explicitement ce que vaut (avec des facteurs genre (-1)^(n/2)) selon la parité de n, idem pour ta somme de départ (ou alors distingue selon n modulo 4 si tu n'as pas envie de te traîner des (-1)^truc).

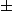
D'une façon générale, évite d'utiliser le signe qui est assez peu rigoureux. Si tu veux vraiment l'utiliser, souviens-toi qu'il ne signifie pas "un coup +, un coup -" mais "parfois +, parfois -". Ainsi il est correct (à la rigueur près) d'écrire et , mais ce n'est pas pour ça que . Dans la même veine, tous les termes de la suite (1,1,1,1,1,1,-1,1,-1,-1,-1,-1,-1,-1,1,1,-1) valent .

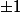
En gros, quand tu vois il faut le lire comme , autrement dit le signe = dans la première proposition est un "faux" et tu ne peux pas permuter les deux membres de l'égalité. Tu rencontreras le même genre d'égalités "asymétriques" quand tu feras des développements limités.

[Kikoo <3 Bieber]

D'accord Skullkid !

[mojosodope]

vous etes des ouf --"