Démontrer que tous les polynômes de second degré peuvent se

[yann06]

bonsoir










après je n'arrive pas à continuer
pouvez vous m'aidez s'il vous plait

[zygomatique]

salut

donc f(x) = a[(x - u)^2 - v]

ensuite moi de même je n'y arrive pas toujours ... puisque ça dépend du signe de v

si v = 0 c'est évidemment fini

si v < 0 alors [(x - u)^2 - v] est de la forme a^2 + b^2 qu'on ne peut pas factoriser dans R (mais dans C)

si v > 0 alors [(x - u)^2 - v] est de la forme a^2 - b^2 ... qu'on peut factoriser dans R

[yann06]

Bonjour zygomatique

tu as dû te tromper de sujet

je n'ai pas parler de v dans le premier message

peux tu m'aider ??

[laetidom]

Bonjour,

Tu veux arriver à ? :

[yann06]

Bonjour Laetidom

oui c'est exactement ça
mais je bloque bien avant ça

peut - tu m'aidez , s'il te plait ?

j'ai vu la démonstration en début d'année mais je ne sais plus la faire

[laetidom]

Ou bloques-tu e x a c t e m e n t . . . ? Car le début de ton calcul me semble correct ! -----> ?

[yann06]

bonjour

avec ,

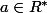
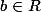
comme a est différent de O , on peut factoriser



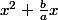
est le début du développement d'une identité remarquable





ensuite je mets au même dénominateur



jusque là -----> c'est OK

[zygomatique]

Bonjour zygomatique

tu as dû te tromper de sujet

je n'ai pas parler de v dans le premier message

peux tu m'aider ??

pas du tout ... mais tu sembles ne pas avoir compris ce que je note u et v pour simplifier ton écriture ...

[laetidom]

bonjour

avec ,

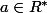
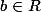
comme a est différent de O , on peut factoriser



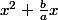
est le début du développement d'une identité remarquable





ensuite je mets au même dénominateur



jusque là -----> c'est OK

et bien si tu dis que :

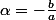
et que

alors = ,

non ?

[yann06]

Bonjour laetidom


jusque là c'est Ok

`
mais pour passer à


c'est là où ça ne va plus

peux tu m'aider ? (s'il te plait )

[danyL]

bjr
- b² + 4ac = - (b² - 4ac)

mais tu as surement trouvé entre temps

[yann06]

Bonjour Danyl

ce que je fait depuis le début d'année ::




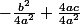
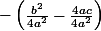
par contre j'ai aussi vu dans un bouquin de première S





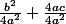
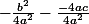
et là , je comprends moins bien

bon samedi

[laetidom]

Salut,

Je ne sais pas d'où vient ta seconde version du livre de 1ère S ? Tu as bien vu que ton calcul aboutit bien à la 1ère version :

Je ne vais pas pouvoir t'aider d'avantage, dsl :

95.JPG (11.9 Kio) Vu 610 fois

[yann06]

Bonsoir Laetidom

merci de m'avoir répondu

je fais exactement comme toi

sur le bouquin de première S
j'avais trouvé ça

[laetidom]

Salut Yann,

Je ne sais pas du tout l'objet de cette notation puisque - par - donne + . . . Peut-être qu'en ayant le scan de la page on pourrait voir le contexte . . . ? Ou une erreur d'impression ? . . .

En tous cas tu as maintenant la première version que tout le monde connaît !

Bonne soirée et @+ sur le forum.