ptitnoir a écrit:Voici une démo , pour expliquer d'où vient
"ce correcteur de biais" :
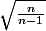
Pour obtenir cette formule à partir d'une échantillon de taille n c'est à dire de
 V.A
V.A 
avec
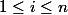
(...)
Cette preuve est correcte lorsque les variables aléatoires sont indépendantes, c'est-à-dire que l'
on réalise successivement n tirages d'une personne dans la population "avec remise", ce qui ne correspond pas totalement à ce qu'est en réalité un sondage. Je m'explique...
ptitnoir a écrit:Bonjour
A partir d'un échantillon de taille n conséquent (
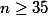
) : par exemple un
sondage de type "oui" ou "non"
je cherche à estimer
sur la population totale :
1) une estimation du nombre de "oui" (ou de "non") sur la population totale ?
2) une estimation de l'écart type de cette estimation ponctuelle de "oui" (ou de "non") sur la population totale
Je connais la formule pour calculer
1) à partir de l'analyse des données de l'échantillon de taille n
mais je ne connais pas la formule qui permet de calculer
2)
Je reviens sur le problème car il me semble qu'il y a peut-être de quoi préciser les choses...
C'est un
sondage (

) sur un
échantillon de taille n dans une population de taille N.
Pour estimer l'écart-type de la population, on va considérer la racine carrée d'un estimateur de la variance de la population.
Or on sait que l'estimateur de la variance de la population consistant à prendre la variance de l'échantillon est un estimateur biaisé.
Il convient donc de rectifier cet estimateur de variance par le bon coefficient.
Et c'est ici qu'on se demande ce qu'est un sondage...
-
Normalement, un sondage c'est un "test" sur des individus différents : on ne teste pas deux fois la même personne (c'est un tirage "simultané" de n personnes, tirage "sans remise"). Du coup, le facteur correctif de l'estimateur de variance est
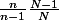
,
d'où l'estimateur de variance
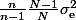
sans biais.
-
Si on laisse l'éventualité de demander plusieurs fois à la même personne (tirages "successifs" de n personnes "avec remise"), alors le facteur correctif de l'estimateur de variance est
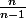
(voir la preuve donnée par ptitnoir),
d'où l'estimateur de variance
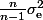
sans biais.
-
Si la population totale est infinie, alors le facteur correctif de l'estimateur de variance est
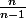
du fait que
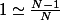
,
d'où l'estimateur de variance
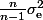
sans biais.

