Equation de variable complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 22 Avr 2015, 09:43
par ArtyB » 22 Avr 2015, 09:43
Bonjour,
Pour résoudre:
^3 -1)((x+i)^5 +i)=0)
On a:
^3 -1)=0)
ou
^5 +i)=0)
Je ne sais pas comment résoudre de façon formelle ces équations mais j'ai remarqué que:
-si je prends x=-2i, alors j'ai
^5 +i)=0)
-si je prends x=2+i, alors j'ai
^3 -1)=0)
Sont-ce là les seules solutions ?
Comment le vérifier ?
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 22 Avr 2015, 09:58
par Manny06 » 22 Avr 2015, 09:58
ArtyB a écrit:Bonjour,
Pour résoudre:
^3 -1)((x+i)^5 +i)=0)
On a:
^3 -1)=0)
ou
^5 +i)=0)
Je ne sais pas comment résoudre de façon formelle ces équations mais j'ai remarqué que:
-si je prends x=-2i, alors j'ai
^5 +i)=0)
-si je prends x=2+i, alors j'ai
^3 -1)=0)
Sont-ce là les seules solutions ?
Comment le vérifier ?
x-i-1 est une des racines cubiques de 1 qui sont 1,j et j²
j=-1/2+iV3/2
j²=-1/2-iV3/2
de même x+i est une des racines 5° de -i
comme -i a pour module 1 et argument -pi/2
les 5 racines 5° ont pour module 1 et argument -pi/10+2kpi/5 avec k entier variant de 0 à 4
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 22 Avr 2015, 10:09
par ArtyB » 22 Avr 2015, 10:09
Merci de votre réponse,
Comment déterminer par le calcul les racines cubiques de 1 ?
De même pour les racines de degré 5 de -i comment savez quel est leur module et argument ?
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 22 Avr 2015, 10:29
par Manny06 » 22 Avr 2015, 10:29
ArtyB a écrit:Merci de votre réponse,
Comment déterminer par le calcul les racines cubiques de 1 ?
De même pour les racines de degré 5 de -i comment savez quel est leur module et argument ?
Il existe un cours sur les racines n° d'un nombre complexe
un nombre complexe non nul de module r et argument t a n racines n°
leur module est racine nIème de r
leur argument
t/n +2kpi/n avec k entier variant de 0 à (n-1)
vous trouverez ceci mieux expliqué sur internet en tapant
racines n-ième d'un nombre complexe
ce sujet est traité en terminale S
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 22 Avr 2015, 10:58
par ArtyB » 22 Avr 2015, 10:58
Les programmes ont dû changé alors parce que quand j'y étais je n'ai jamais fait ça (c'était il n'y a pas si longtemps pourtant, en 2013). Merci en tous cas, je vais regarder ça de plus prés.
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 22 Avr 2015, 13:02
par ArtyB » 22 Avr 2015, 13:02
D'accord, alors voilà ce que j'ai trouvé, les racine n-ième d'un nombre complexe Z sont de la forme:

Avec:
-R module de Z
-

argument de Z
Donc ici si je prends Z=1, j'ai son argument=0 et module=1
d'où racine n-ieme=

Ici n=3 d'où :
racine n-ième=

racine n-ième=

et ensuite ?
Si je prends Z=i j'ai argument=

et module=1
d'où racine n-ième=

Ici n=5 d'où
racine n-ième=

racine n-ième=

Et ensuite ?
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 22 Avr 2015, 13:14
par Manny06 » 22 Avr 2015, 13:14
ArtyB a écrit:D'accord, alors voilà ce que j'ai trouvé, les racine n-ième d'un nombre complexe Z sont de la forme:

Avec:
-R module de Z
-

argument de Z
Donc ici si je prends Z=1, j'ai son argument=0 et module=1
d'où racine n-ieme=\sqrt[n]{1} e^{i\frac{0}{n} +\frac{2k\pi}{n}}
Si je prends Z=i j'ai argument=

et module=1
d'où racine n-ièe=\sqrt[n]{1} e^{i\frac{\frac{\pi}{2}}{n} +\frac{2k\pi}{n}}
je n'arrive pas à lire ton écriture
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 22 Avr 2015, 13:35
par ArtyB » 22 Avr 2015, 13:35
Au temps pour moi, je faisais des modifications c'est peut être pour ça, ça marche là ?
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 22 Avr 2015, 13:44
par Manny06 » 22 Avr 2015, 13:44
ArtyB a écrit:Au temps pour moi, je faisais des modifications c'est peut être pour ça, ça marche là ?
attention dans toutes les écritures d'exposant i est en facteur
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 22 Avr 2015, 14:39
par ArtyB » 22 Avr 2015, 14:39
Ah oui au temps pour moi, j'avais totalement oublié. Voilà c'est modifié !
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 22 Avr 2015, 23:44
par ArtyB » 22 Avr 2015, 23:44
Mais du coup une fois que l'on a ces formes de racines n-ièmes on en fait quoi ?
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 23 Avr 2015, 16:29
par ArtyB » 23 Avr 2015, 16:29
Personne pour me guider ? :(
-
mathelot
 par mathelot » 23 Avr 2015, 17:29
par mathelot » 23 Avr 2015, 17:29
ArtyB a écrit:On a:
^5 +i)=0)
Je ne sais pas comment résoudre de façon formelle ces équations mais j'ai remarqué que:
-si je prends x=-2i, alors j'ai
^5 +i)=0)
bien vû.
appelons z_0 cette racine -2i
^5 =-i)
^5 =-i)
en quotientant membres à membres
^5 = 1)

est donc une racine 5ème de l'unité.
Les cinq racines de l'unité sont supposées connues (car
=\frac{\sqrt{5}-1}{4})
et
=\frac{\sqrt{5}+1}{4})
)
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 23 Avr 2015, 17:48
par fibonacci » 23 Avr 2015, 17:48
Aussi...
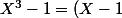(X^2+X+1))
\,\left(X^2+X+1\right)=\left(x-i-2\right)\,\left( \left(x-i-1\right)^2+x-i\right))
d'où les
racines:
\,i}\over{2}} , x_2={{\left( \sqrt{3}+2\right)\,i+1}\over{2}} , x_3=i+2 \right])
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 23 Avr 2015, 17:55
par ArtyB » 23 Avr 2015, 17:55
Waow ça m'a l'air bien compliqué tout ça.
Je suis d'accord sur le fait que ça soit une racine 5ème de l'unité mais en quoi ça nous sert ici ?
En fait ce que je ne comprends pas c'est la méthode à adopter pour résoudre cet exercice, comment faut il procéder ?
-
mathelot
 par mathelot » 23 Avr 2015, 18:04
par mathelot » 23 Avr 2015, 18:04
ArtyB a écrit:Waow ça m'a l'air bien compliqué tout ça.
Je suis d'accord sur le fait que ça soit une racine 5ème de l'unité mais en quoi ça nous sert ici ?
En fait ce que je ne comprends pas c'est la méthode à adopter pour résoudre cet exercice, comment faut il procéder ?
soit
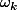
la racine 5eme générique.
si

est une racine particulière (ici -2i) les autres racines sont obtenues par
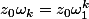
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 23 Avr 2015, 18:17
par ArtyB » 23 Avr 2015, 18:17
Alors c'est pire que tout, j'ai beau avoir lu et relu mon cours sur les racine n-ièmes je ne comprends pas du tout ce que vous faîtes là.
"racine n-ième générique" ça veut dire quoi ?
Et qu'est-ce que

?
-
mathelot
 par mathelot » 23 Avr 2015, 18:22
par mathelot » 23 Avr 2015, 18:22
ArtyB a écrit:Alors c'est pire que tout, j'ai beau avoir lu et relu mon cours sur les racine n-ièmes je ne comprends pas du tout ce que vous faîtes là.
"racine n-ième générique" ça veut dire quoi ?
Et qu'est-ce que

?
oui, ça signifie "forme générale des racines"
5 est premier. elles sont toutes de la forme

avec i=0,1...4
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 23 Avr 2015, 18:39
par ArtyB » 23 Avr 2015, 18:39
Ah d'accord, merci , mais la forme générale des racines c'est bien:

et là vous dîtes que c'est:
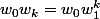
ce qui revient à dire:
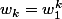
et je ne comprends pas ce que cela veut dire.
En fait c'est vraiment la méthode qui me manque je ne sais pas quoi faire quand je suis devant mon équation, à part
1) egaliser chaque expression entre paranthèse à 0
2) chercher des solutions évidentes
Quelle est la méthode pour trouver la forme des solutions générales ? Et comment résoudre cet exercice de manière rigoureuse ?
-
mathelot
 par mathelot » 23 Avr 2015, 20:10
par mathelot » 23 Avr 2015, 20:10
soit
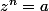
(1) et

une solution
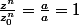
^n =1)
les solutions de (1) sont

(pour k=0,1...n-1) où
^n=1)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
ou
argument de Z
et module=1
?