Divisibilite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
PapyRusse
- Membre Naturel
- Messages: 25
- Enregistré le: 12 Déc 2013, 17:13
-
 par PapyRusse » 12 Déc 2013, 17:23
par PapyRusse » 12 Déc 2013, 17:23
Salut,
Je cherche a savoir pour quelle valeur de k
(2k+1)! divise produit ((3i)^2 -1) i variant de 1 a k
Je donne un exemple pour eviter toute confusion vu que ce n`est pas ecrit en latex
Exemple k=3
(2*3+1)!=7!=5040
produit ((3i)^2 -1) i variant de 1 a 3 = 8*35*80=22040
Pour k=3
(2*3+1)! ne divise pas produit ((3i)^2 -1) i variant de 1 a 3
Merci pour tout eclairage.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 12 Déc 2013, 17:37
par arnaud32 » 12 Déc 2013, 17:37
indication: (3i)²-1=(3i+1)(3i-1)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 12 Déc 2013, 17:48
par Ben314 » 12 Déc 2013, 17:48
Salut,
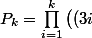^2-1\big)=\prod_{i=1}^{k}\frac{3i(3i-1)(3i+1)}{3i}=\frac{(3k+1)!}{3^k.k!}\)
donc
!\,|\,P_k\ \Leftrightarrow\ 3^k\,|\,\frac{(3k+1)!}{k!(2k+1)!}={3k+1 \choose k}=C_k\)
(coeff. binomial) Ce qui signifie que la valuation triadique
)
(exposant de 3 dans la décomposition en nombres premiers de
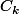
) doit être

.
Or, pour tout p premier et tout entier n, il est façile de vérifier que
=\sum_{i\geq 1}\lfloor\frac{n}{p^i}\rfloor)
donc
<br />=\sum_{i\geq 1}\Big(\lfloor\frac{3k+1}{3^i}\rfloor-\lfloor\frac{2k+1}{3^i}\rfloor-\lfloor\frac{k}{3^i}\rfloor\Big)<br />=\sum_{i\geq 1}\Big(\lfloor\frac{k}{3^{i-1}}\rfloor-\lfloor\frac{2k+1}{3^i}\rfloor-\lfloor\frac{k}{3^i}\rfloor\Big)<br />=k-\sum_{i\geq 1}\lfloor\frac{2k+1}{3^i}\rfloor)
donc...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
PapyRusse
- Membre Naturel
- Messages: 25
- Enregistré le: 12 Déc 2013, 17:13
-
 par PapyRusse » 12 Déc 2013, 18:30
par PapyRusse » 12 Déc 2013, 18:30
Merci pour la preuve.
Si j`ai bien compris aucune valeur de k ne permet la divisibilite.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 12 Déc 2013, 19:23
par Ben314 » 12 Déc 2013, 19:23
PapyRusse a écrit:Merci pour la preuve.
Si j`ai bien compris aucune valeur de k ne permet la divisibilite.
Oui... sauf si je me suis gourré dans les calculs...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
PapyRusse
- Membre Naturel
- Messages: 25
- Enregistré le: 12 Déc 2013, 17:13
-
 par PapyRusse » 13 Déc 2013, 02:10
par PapyRusse » 13 Déc 2013, 02:10
Ben314 a écrit:Oui... sauf si je me suis gourré dans les calculs...
Y a toujours un doute la?
-
MMu
- Membre Relatif
- Messages: 399
- Enregistré le: 11 Déc 2011, 22:43
-
 par MMu » 13 Déc 2013, 05:51
par MMu » 13 Déc 2013, 05:51
PapyRusse a écrit:Y a toujours un doute la?
Il n'y a aucun doute. Trivial :
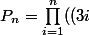^2-1))
n'est pas divisible par
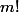
(
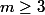
) puisque
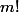
est divisible par

mais

ne l'est pas
.. :lol3: ..:zen: .

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 13 Déc 2013, 08:09
par Ben314 » 13 Déc 2013, 08:09
MMu a écrit:Il n'y a aucun doute. Trivial :
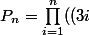^2-1))
n'est pas divisible par
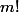
(
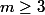
) puisque
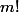
est divisible par

mais

ne l'est pas
.. :lol3: ..:zen: .
Vu comme ça, il y a... moins de risque d'erreurs... :lol3:
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
PapyRusse
- Membre Naturel
- Messages: 25
- Enregistré le: 12 Déc 2013, 17:13
-
 par PapyRusse » 13 Déc 2013, 14:43
par PapyRusse » 13 Déc 2013, 14:43
Merci pour la clarte.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
