Démontrer qu'une somme de deux suite donne une suite géométrique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
MAIS_DIT
- Membre Naturel
- Messages: 75
- Enregistré le: 30 Sep 2012, 10:38
-
 par MAIS_DIT » 10 Sep 2013, 18:57
par MAIS_DIT » 10 Sep 2013, 18:57
Bonjours à tous et bonne rentrée !
J'ai un exercice de maths sur les suites, mais celui ci me pose une grosse colle :mur:
Je n'arrive plus à savoir comment prouver si une somme de suite est géométrique !!
Je m'explique .
J'ai la suite définie par u(0)=2 et u(n+1)= 2u(n)-v(n)
ainsi que la suite définie par v(0)=-1 et v(n+1)=u(n)+4v(n)
Puis on me dit que je dois prouver que la suite p(n) définie par p(n)=u(n)+v(n) est géométrique !!!
Quelqu'un aurait il l'amabilité de m'indiquer la méthode ?
Merci !
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 10 Sep 2013, 19:28
par Carpate » 10 Sep 2013, 19:28
MAIS_DIT a écrit:Bonjours à tous et bonne rentrée !
J'ai un exercice de maths sur les suites, mais celui ci me pose une grosse colle :mur:
Je n'arrive plus à savoir comment prouver si une somme de suite est géométrique !!
Je m'explique .
J'ai la suite définie par u(0)=2 et u(n+1)= 2u(n)-v(n)
ainsi que la suite définie par v(0)=-1 et v(n+1)=u(n)+4v(n)
Puis on me dit que je dois prouver que la suite p(n) définie par p(n)=u(n)+v(n) est géométrique !!!
Quelqu'un aurait il l'amabilité de m'indiquer la méthode ?
Merci !
Calcule
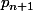
et le résultat que tu obtiendras s'exprimera en fonction de
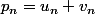
-
MAIS_DIT
- Membre Naturel
- Messages: 75
- Enregistré le: 30 Sep 2012, 10:38
-
 par MAIS_DIT » 10 Sep 2013, 19:39
par MAIS_DIT » 10 Sep 2013, 19:39
Carpate a écrit:Calcule
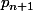
et le résultat que tu obtiendras s'exprimera en fonction de
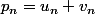
Coucou, je suis désolé mais malgré l'explication que tu m'as fournie j'ai un peu du mal à comprendre :hein: tu pourrais m'aider un petit plus s'il te plait ? merci beaucoup !
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 10 Sep 2013, 19:44
par Carpate » 10 Sep 2013, 19:44
MAIS_DIT a écrit:Coucou, je suis désolé mais malgré l'explication que tu m'as fournie j'ai un peu du mal à comprendre :hein: tu pourrais m'aider un petit plus s'il te plait ? merci beaucoup !
Que donne
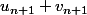
?
-
MAIS_DIT
- Membre Naturel
- Messages: 75
- Enregistré le: 30 Sep 2012, 10:38
-
 par MAIS_DIT » 10 Sep 2013, 20:00
par MAIS_DIT » 10 Sep 2013, 20:00
Carpate a écrit:Que donne
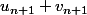
?
je trouve
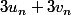
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 11 Sep 2013, 07:24
par Carpate » 11 Sep 2013, 07:24
MAIS_DIT a écrit:je trouve
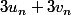
C'est à dire
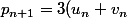= ...)
Ca aurait dû t'interpeler tout de suite !
-
MAIS_DIT
- Membre Naturel
- Messages: 75
- Enregistré le: 30 Sep 2012, 10:38
-
 par MAIS_DIT » 11 Sep 2013, 12:33
par MAIS_DIT » 11 Sep 2013, 12:33
Carpate a écrit:C'est à dire
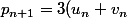= ...)
Ca aurait dû t'interpeler tout de suite !
Oh c'est vrai ! Je n'y ai meme pas fait attention, merci !
-
MAIS_DIT
- Membre Naturel
- Messages: 75
- Enregistré le: 30 Sep 2012, 10:38
-
 par MAIS_DIT » 11 Sep 2013, 12:42
par MAIS_DIT » 11 Sep 2013, 12:42
Carpate a écrit:C'est à dire
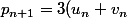= ...)
Ca aurait dû t'interpeler tout de suite !
Mais par contre comment dois je faire pour ensuite exprimer p(n) en fonction de n ??
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 11 Sep 2013, 14:13
par Carpate » 11 Sep 2013, 14:13
MAIS_DIT a écrit:Mais par contre comment dois je faire pour ensuite exprimer p(n) en fonction de n ??
Cours : expression du terme

d'une suite géométrique de raison q et de premier terme

-
MAIS_DIT
- Membre Naturel
- Messages: 75
- Enregistré le: 30 Sep 2012, 10:38
-
 par MAIS_DIT » 11 Sep 2013, 14:23
par MAIS_DIT » 11 Sep 2013, 14:23
Carpate a écrit:Cours : expression du terme

d'une suite géométrique de raison q et de premier terme

Dans une suite géométrique,
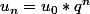
Donc sachant que
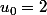
et
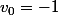
et que
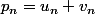
Alors :
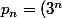 * (u_0 + v_0))
???
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 11 Sep 2013, 14:34
par Carpate » 11 Sep 2013, 14:34
MAIS_DIT a écrit:Dans une suite géométrique,
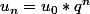
Donc sachant que
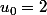
et
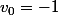
et que
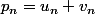
Alors :
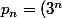 * (u_0 + v_0))
???
Oui, pourquoi hésites-tu ? Et tu peux même te risquer à calculer
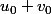
-
MAIS_DIT
- Membre Naturel
- Messages: 75
- Enregistré le: 30 Sep 2012, 10:38
-
 par MAIS_DIT » 11 Sep 2013, 14:45
par MAIS_DIT » 11 Sep 2013, 14:45
Carpate a écrit:Oui, pourquoi hésites-tu ? Et tu peux même te risquer à calculer
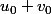
J'ai une grosse hésitation parce que ça ne concordait pas avec la question suivante... je m'explique ;
"à l'aide du résultat trouvé précédemment, montrer que, pour tout entier naturel n,
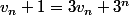
Et la je cafouille complètement... j'ai
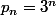
donc,
_ =u_(n+1)+v_(n+1))
 = p_(n+1) - u_(n+1))
problème, je connais

mais pas
)
!! comment faire ?
-
MAIS_DIT
- Membre Naturel
- Messages: 75
- Enregistré le: 30 Sep 2012, 10:38
-
 par MAIS_DIT » 11 Sep 2013, 14:46
par MAIS_DIT » 11 Sep 2013, 14:46
Carpate a écrit:Oui, pourquoi hésites-tu ? Et tu peux même te risquer à calculer
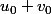
Enfin si, je connais
)
, on a vu tout à l'heure que sa donnait
)
mais au final, je n'arrive pas a trouver
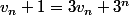
:/ :mur: :mur: :mur:
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 11 Sep 2013, 14:51
par Carpate » 11 Sep 2013, 14:51
MAIS_DIT a écrit:J'ai une grosse hésitation parce que ça ne concordait pas avec la question suivante... je m'explique ;
"à l'aide du résultat trouvé précédemment, montrer que, pour tout entier naturel n,
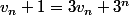
Et la je cafouille complètement... j'ai
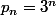
donc,
_ =u_(n+1)+v_(n+1))
 = p_(n+1) - u_(n+1))
problème, je connais

mais pas
)
!! comment faire ?
v
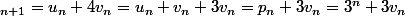
-
MAIS_DIT
- Membre Naturel
- Messages: 75
- Enregistré le: 30 Sep 2012, 10:38
-
 par MAIS_DIT » 11 Sep 2013, 14:53
par MAIS_DIT » 11 Sep 2013, 14:53
Carpate a écrit:v
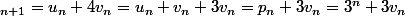
Oh bah mince, c'était vraiment évident en fin de compte :doh: :doh: ... Merci beaucoup pour ton aide !
-
MAIS_DIT
- Membre Naturel
- Messages: 75
- Enregistré le: 30 Sep 2012, 10:38
-
 par MAIS_DIT » 11 Sep 2013, 15:05
par MAIS_DIT » 11 Sep 2013, 15:05
Carpate a écrit:v
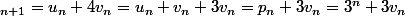
Enfait j'ai juste une dernière question !
Je voudrais juste savoir comment prouver que la suite définie par
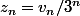
est arithmétique après j'arrête de t'embêter promis ! :we:
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 11 Sep 2013, 16:20
par Carpate » 11 Sep 2013, 16:20
MAIS_DIT a écrit:Enfait j'ai juste une dernière question !
Je voudrais juste savoir comment prouver que la suite définie par
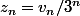
est arithmétique après j'arrête de t'embêter promis ! :we:
Quelle est la relation attendue entre
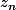
et
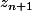
?
Je voulais dire que trouve-tu pour
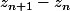
?
-
MAIS_DIT
- Membre Naturel
- Messages: 75
- Enregistré le: 30 Sep 2012, 10:38
-
 par MAIS_DIT » 11 Sep 2013, 19:32
par MAIS_DIT » 11 Sep 2013, 19:32
Carpate a écrit:Quelle est la relation attendue entre
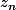
et
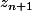
?
Je voulais dire que trouve-tu pour
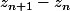
?
j'ai donc
/(3^n+1) - v_n/3n)
mais comment simplifier pour trouver la raison r ?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 11 Sep 2013, 19:42
par Carpate » 11 Sep 2013, 19:42
-
MAIS_DIT
- Membre Naturel
- Messages: 75
- Enregistré le: 30 Sep 2012, 10:38
-
 par MAIS_DIT » 11 Sep 2013, 19:44
par MAIS_DIT » 11 Sep 2013, 19:44
Ah d'accord !!! merci beaucoup !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 99 invités
