Topologie....ouvert ou fermé
22 messages
- Page 1 sur 2 - 1, 2
Topologie....ouvert ou fermé
A={(x,y) /in R² tq |x|<1 |y|<=1} est un ouvert? un fermé?
on peut expliciter un peu A: A=]-1,1[x]-1,1]
Vu comme ça, conjecture = c'est ni un ouvert ni un fermé, encore faut il le prouver.
C'est pas un ouvert, sinon pour tout y de ]-1,1] on peut trouver une boule de rayon r>0 et de centre (x,y) incluse dans A. Ca n'est pas le cas quand y=1. Comment je peux écrire ça proprement? je dois prendre une norme au pif et voir ce que ça donne (trouver un point qui déborde de A tout en étant dans la boule)?
pareil pour A non fermé. A non fermé <=>C(R²,A) (complémentaire de A dans R²) ouvert.
mais C(R²,A)=(]-oo,1]U[-1,+oo[)x(]-oo,1]U]-1,+oo[) et on utilise le même argument que précédement.
on peut expliciter un peu A: A=]-1,1[x]-1,1]
Vu comme ça, conjecture = c'est ni un ouvert ni un fermé, encore faut il le prouver.
C'est pas un ouvert, sinon pour tout y de ]-1,1] on peut trouver une boule de rayon r>0 et de centre (x,y) incluse dans A. Ca n'est pas le cas quand y=1. Comment je peux écrire ça proprement? je dois prendre une norme au pif et voir ce que ça donne (trouver un point qui déborde de A tout en étant dans la boule)?
pareil pour A non fermé. A non fermé <=>C(R²,A) (complémentaire de A dans R²) ouvert.
mais C(R²,A)=(]-oo,1]U[-1,+oo[)x(]-oo,1]U]-1,+oo[) et on utilise le même argument que précédement.
eratos a écrit:A={(x,y) /in R² tq |x|0 et de centre (x,y) incluse dans A. Ca n'est pas le cas quand y=1. Comment je peux écrire ça proprement? je dois prendre une norme au pif et voir ce que ça donne (trouver un point qui déborde de A tout en étant dans la boule)?
pareil pour A non fermé. A non fermé C(R²,A) (complémentaire de A dans R²) ouvert.
mais C(R²,A)=(]-oo,1]U[-1,+oo[)x(]-oo,1]U]-1,+oo[) et on utilise le même argument que précédement.
salut
pour non ouvert
tu prends le point M(0,1)
quelle que soit la boule de centre M et de rayon r>0, le point (0,1+r/2) est dans cette boule mais pas dans A
pour non fermé, tu prends N(1,0) pour montrer que le complémentaire n'est pas ouvert
chan79 a écrit:salut
pour non ouvert
tu prends le point M(0,1)
quelle que soit la boule de centre M et de rayon r>0, le point (0,1+r/2) est dans cette boule mais pas dans A
pour non fermé, tu prends N(1,0) pour montrer que le complémentaire n'est pas ouvert
Merci pour vos réponse.
Un autre problème:
compact ou pas? {(x,y) \in R² , x²+xy+y²<=1}
Faut montrer si c'est fermé et borné ou pas.... mais une expression comme ça c'est pas évident à manipuler. J'essaie de la transformer depuis tout à l'heure, j'arrive pas à avoir un truc simple :marteau:
Oui: chrono trigger ça poutre :lol3:
eratos a écrit:La frontière de Q serait donc R :doh:
Tout à fait :++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
eratos a écrit:Merci pour vos réponse.
Un autre problème:
compact ou pas? {(x,y) \in R² , x²+xy+y²<=1}
Faut montrer si c'est fermé et borné ou pas.... mais une expression comme ça c'est pas évident à manipuler. J'essaie de la transformer depuis tout à l'heure, j'arrive pas à avoir un truc simple :marteau:
Oui: chrono trigger ça poutre :lol3:
Fermé : tu le démontrer en utisant la continuité ou les suites.
Borné : Passe en ccordonées polaires
Le point
En remarquant
Salut
Je souhaite montrer ça:
X est l'espace topologique discret si et ssi {x} est ouvert pour tout x dans X
sens direct: les singletons {x} sont tous dans l'ensemble P(X) des parties de X, donc sont par définition ouverts.
sens indirect: là je vois pas comment faire, en fait avec tout les singletons on peut construire la topologie(X, P(X)) en les réunissant (les singletons) de toutes les manières possibles.
Ou alors on construit une topologie avec les singletons et on montre que c'est la discrète ce qui revient au même :marteau:
Merci Mohamed :lol3:
Je souhaite montrer ça:
X est l'espace topologique discret si et ssi {x} est ouvert pour tout x dans X
sens direct: les singletons {x} sont tous dans l'ensemble P(X) des parties de X, donc sont par définition ouverts.
sens indirect: là je vois pas comment faire, en fait avec tout les singletons on peut construire la topologie(X, P(X)) en les réunissant (les singletons) de toutes les manières possibles.
Ou alors on construit une topologie avec les singletons et on montre que c'est la discrète ce qui revient au même :marteau:
Merci Mohamed :lol3:
sens indirect: là je vois pas comment faire, en fait avec tout les singletons on peut construire la topologie(X, P(X)) en les réunissant (les singletons) de toutes les manières possibles.
ben oui, tu gommes ton "là je vois pas comment faire", tu dis le reste et t'as fini.
Formellement, tu dois montrer que si T est une topologie sur X qui contient tous les singletons, alors T = P(X). Comme tu l'as si bien dit, si A est une partie de X, A est la réunion pour x dans A des {x}. Les {x} sont dans T, et T est une topologie, donc A est dans T. Donc T = P(X).
On munit X de la topologie discrete et on prend une partie A de X.
on cherche quels sont les fermés de A, l'interieur de A, les voisinages de x dans A, l'adherence de A
Li'ntérieur de A est A lui même car il est ouvert.
J'avais trouvé que le seule voisinage d'un point x de X était {x}, je l'avais fait hier soir avant de me coucher, je me souviens plus... (*)
l'adherence de A c'est l'ensemble {x X tq
X tq  V voisinage de x, VnA non vide}
V voisinage de x, VnA non vide}
mais en prenant x dans X, VnA={x}nA est non vide que si x est dans A, autrement dit que l'adherence de A c'est A.
La topologie c'est bizarre, alors peut etre que l'interieur et la fermeture peuvent coincider. Après tout l'ensemble vide et X eux même sont fermés et ouvert à la fois.
Quand au fermés de A, je ne vois pas.
edit:(*){x} est bien un voisinage de x mais ce n'est pas le seul, c'est juste le plus "petit".
on cherche quels sont les fermés de A, l'interieur de A, les voisinages de x dans A, l'adherence de A
Li'ntérieur de A est A lui même car il est ouvert.
J'avais trouvé que le seule voisinage d'un point x de X était {x}, je l'avais fait hier soir avant de me coucher, je me souviens plus... (*)
l'adherence de A c'est l'ensemble {x
mais en prenant x dans X, VnA={x}nA est non vide que si x est dans A, autrement dit que l'adherence de A c'est A.
La topologie c'est bizarre, alors peut etre que l'interieur et la fermeture peuvent coincider. Après tout l'ensemble vide et X eux même sont fermés et ouvert à la fois.
Quand au fermés de A, je ne vois pas.
edit:(*){x} est bien un voisinage de x mais ce n'est pas le seul, c'est juste le plus "petit".
Il n'y a rien à voir, il faut juste appliquer la définition de fermé, puis la définition de être ouvert pour la topologie discrète :
A est fermé <=> le complémentaire de A est ouvert <=> vrai.
Toutes les parties de X sont fermées. Et elles sont toutes ouvertes. C'est vrai que le vocabulaire n'est pas forcément très adapté.
A est fermé <=> le complémentaire de A est ouvert <=> vrai.
Toutes les parties de X sont fermées. Et elles sont toutes ouvertes. C'est vrai que le vocabulaire n'est pas forcément très adapté.
Re:
(X,O) un espace topologique, A et B c O AcB
Montrer que si A est une base d'ouvert, alors B est aussi une base d'ouvert.
Donc, soit U un ouvert de X, U est réunion d'élément de A, donc réunion d'élément de B.. B est donc une base d'ouvert de X
On veut montrer que les intervalles ouverts forment une base d'ouverts de R.
on note B cette base: B= {]a,b[, (a,b)², a
Par suite (on munit R d'"une" topologie), il faut montrer que les intervalles ]a,b[ sont ouverts quels que soient a et b de R, a
En faisant un petit schema, j'ai trouvé B(x,r) avec r=min(|x-a|,|x-b|)
Là j'ai un petit problème technique :zen: , c'est un peu un melimelo des notions d'espace métrique et d'espace topologique. Comment alors faire une vraie preuve (en admettant que c'est pas que des conneries que j'ai écrit)?
(X,O) un espace topologique, A et B c O AcB
Montrer que si A est une base d'ouvert, alors B est aussi une base d'ouvert.
Donc, soit U un ouvert de X, U est réunion d'élément de A, donc réunion d'élément de B.. B est donc une base d'ouvert de X
On veut montrer que les intervalles ouverts forment une base d'ouverts de R.
on note B cette base: B= {]a,b[, (a,b)², a
Par suite (on munit R d'"une" topologie), il faut montrer que les intervalles ]a,b[ sont ouverts quels que soient a et b de R, a
En faisant un petit schema, j'ai trouvé B(x,r) avec r=min(|x-a|,|x-b|)
Là j'ai un petit problème technique :zen: , c'est un peu un melimelo des notions d'espace métrique et d'espace topologique. Comment alors faire une vraie preuve (en admettant que c'est pas que des conneries que j'ai écrit)?
Bonjour
Soit)
) un espace métrique, alors les boules ouvertes forment une base de
un espace métrique, alors les boules ouvertes forment une base de ) .
.
Si on peut démontrer cette propriété pour) , on l'a automatiquement pour
, on l'a automatiquement pour 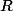 .
.
Pour (1) Il suffit de se rappeler qu'un ouvert A est voisinage de chacun de ses points et pour le cas de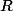 juste se rappeler qu'un intervalle ouvert borné ]a,b[ est une boule ouverte de centre .... et de rayon r=.....? et qu'un intervalle ouvert non borné est lui même un ouvert.
juste se rappeler qu'un intervalle ouvert borné ]a,b[ est une boule ouverte de centre .... et de rayon r=.....? et qu'un intervalle ouvert non borné est lui même un ouvert.
Autre indication: Adapte la démonstration faite pour la topologie discrète à celle de (1) en faisant jouer le rôle des singletons aux boules ouvertes.
eratos a écrit: On veut montrer que les intervalles ouverts forment une base d'ouverts de.
Soit
Si on peut démontrer cette propriété pour
Pour (1) Il suffit de se rappeler qu'un ouvert A est voisinage de chacun de ses points et pour le cas de
Autre indication: Adapte la démonstration faite pour la topologie discrète à celle de (1) en faisant jouer le rôle des singletons aux boules ouvertes.
Bonjour
Si R est muni sa topologie usuelle, il suffit juste de rappeler qu'un intervalle ouvert borné ]a,b[ est lui-même une boule ouverte (de centre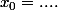 et de rayon
et de rayon  et qu'on peut prendre uniquement les intervalles ouverts bornés.
et qu'on peut prendre uniquement les intervalles ouverts bornés.
Remarque: C"est un résultat valable dans un espace métrique (E,d) au sens les boules ouverte forment une base de (E,d) (de démonstration plus ou moins facile si l'on se rappelle la caractérisation d'un ouvert de (E,d)).
eratos a écrit: On veut montrer que les intervalles ouverts forment une base d'ouverts de R.
Si R est muni sa topologie usuelle, il suffit juste de rappeler qu'un intervalle ouvert borné ]a,b[ est lui-même une boule ouverte (de centre
Remarque: C"est un résultat valable dans un espace métrique (E,d) au sens les boules ouverte forment une base de (E,d) (de démonstration plus ou moins facile si l'on se rappelle la caractérisation d'un ouvert de (E,d)).
Bonjour
Dans la démonstration que tu as ébauchée, tu as parlé de boule B(x,r), tu as donc muni (inconsciemment peut-être) R d'une structure d'espace métrique.
Si R est muni de sa topologie usuelle, il suffit juste de se rappeler qu'un intervalle ouvert borné ]a,b[ est lui-même une boule ouverte (de centre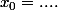 et de rayon
et de rayon  ) et qu'on peut prendre uniquement les intervalles ouverts bornés.
) et qu'on peut prendre uniquement les intervalles ouverts bornés.
Remarque: C"est un résultat valable dans un espace métrique (E,d) au sens les boules ouvertes forment une base de (E,d) (de démonstration plus ou moins facile si l'on se rappelle la caractérisation d'un ouvert de (E,d)).
eratos a écrit: On veut montrer que les intervalles ouverts forment une base d'ouverts de R.
Dans la démonstration que tu as ébauchée, tu as parlé de boule B(x,r), tu as donc muni (inconsciemment peut-être) R d'une structure d'espace métrique.
Si R est muni de sa topologie usuelle, il suffit juste de se rappeler qu'un intervalle ouvert borné ]a,b[ est lui-même une boule ouverte (de centre
Remarque: C"est un résultat valable dans un espace métrique (E,d) au sens les boules ouvertes forment une base de (E,d) (de démonstration plus ou moins facile si l'on se rappelle la caractérisation d'un ouvert de (E,d)).
Bonjour.
Autre remarque:
1) On peut se restreindre pour le cas d'un espace métrique (E,d) aux boules de rayon r < M et en particulier pour M=1
2) On comprend alors aisément que les singletons forment un base pour la topologie discrète car celle-ci est métrisable, on définit d par=0) si
si  et
et =1) si
si 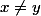 , pour
, pour 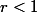 , on a alors
, on a alors =\{x\})
Autre remarque:
1) On peut se restreindre pour le cas d'un espace métrique (E,d) aux boules de rayon r < M et en particulier pour M=1
2) On comprend alors aisément que les singletons forment un base pour la topologie discrète car celle-ci est métrisable, on définit d par
22 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 115 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
