Un singleton est un fermé.

[abcd22]

Ça ne démontre rien, d'où sort cette égalité ?

Qui n'est rien d'autre que écrit d'une façon différente.

[HanZel]

Ça ne démontre rien, d'où sort cette égalité ?

Soit ,
Or (là on entre dans le contexte où )
Et donc puisque ceci est vrai pour tout y de la boule.

Je suis désolé, j'insiste mais est ce que ça serait valable?

Merci pour ta réponse :++:

[abcd22]

Soit ,
Or (là on entre dans le contexte où )
Et donc .

Tu montres que , mais tu ne montres pas que est un fermé, c'est vrai et c'est pour ça qu'on note les boules fermées de la même façon que l'adhérence (mais je pense que la notation qu'on utilisait quand j'étais en prépa avec un crochet fermé ou ouvert à droite était mieux car elle n'entretenait pas cette confusion), mais ce n'est pas démontré (à moins que tu l'aies fait ailleurs dans ton cours...).

[HanZel]

Soit (Je sous-entend la boule fermée)
Or (là on entre dans le contexte où d(x,y)=0) Et donc

(En oubliant l'idée de l'adhérence que j'avais prise au départ)

La je ne prouve pas que {x} est une boule fermée? Parce que j'ai quand même explicité la distance inférieure OU égale (définition de la boule fermée) dans

Je suis vraiment désolé de toutes ces questions mais je n'arrive pas à voir où je fais une erreur
Le problème est de savoir si une boule fermée est un fermé? Si c'est le cas, ça va, je pense que j'ai compris...

[fourize]

bonsoir !

maintenant je suis bien armé :zen:
on sait que, parmi les méthodes pour montrer qu'un ensemble X est fermé, est de montrer que "s'il existe une suite convergente de X, alors converge vers un x de X".

raisonnant ainsi, la suite = x cte donc converge vers lui meme. ce qu'il fallait démontrer et donc le singleton est un fermé !

[abcd22]

raisonnant ainsi, la suite = x cte donc converge vers lui meme.

Il faut dire que l'espace est séparé pour avoir l'unicité de la limite.

[fourize]

re,

Il faut dire que l'espace est séparé pour avoir l'unicité de la limite.

:doh: explique !

pourtant je sais bien que si la limite d'une suite existe elle est unique !
et ici notre suite est cte ! donc admet bien une limite (unique )
comment veut tu qu'elle ne soit pas unique ! (un contre exemple si possible )

[kazeriahm]

Cf wikipedia http://fr.wikipedia.org/wiki/Espace_s%C3%A9par%C3%A9

[HanZel]

J'ai trouvé avec le complémentaire !
... enfin j'espère...

Soit

(On pose une boule ouverte appartenant au complémentaire de {x} dans E)

Soit
donc on a :
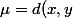(ici ) telle que . Le complémentaire de {x} dans E est donc un ouvert, donc {x} est un fermé !

Je crois que si c'est toujours pas ça... je vais me chercher une corde ! :ptdr:

Ça serait trop beau qu'il n'y ait rien à redire, qu'est ce qui ne va pas dans cette démo là?

[HanZel]

Je ne vois pas comment tu peux affirmer cela !

Réduis le rayon de ta boule de moitié et l'inégalité triangulaire te permet de conclure ...

Non tu as quand même raison, j'avais fait une faute de frappe mais je viens de la rectifier. (j'avais écrit d(x,y)<d(x,y) je voulais écrire d(y,z)<d(x,y) puisque c'est z qui appartient à la boule de centre y de rayon d(x,y)).

Merci de m'avoir rectifié à ton insu :happy2:

Sinon est ce que là j'ai bien prouvé qu'un singleton était un fermé, ou il y a encore une chose non démontrée ou non cohérente?

[HanZel]

D'accord, merci !

[Finrod]

Il faut le démontrer avec des boules, au moins une fois.

Philosophiquement parlant, une espace métrique est toujours séparé et ses points sont donc fermés par définition de l'adhérence.

En effet l'adhérence d'un espace X est l'ensemble des points qui vérifient chacun que tout ouvert le contenant intersecte X. Ici cela revient à dire "contient x" donc cela revient à la définition de séparabilité.

Bien entendu je dis "philosophiquement" car il y a de la "triche". Montrer qu'un espace métrique est séparé n'est pas totalement évident et se fait aussi avec des boules.

[khater]

Hanzel , déjà l’inégalité de cauchy-shwartz c'est d(x,y)+d(y,z)>=d(x,z) et c'est pas un moin ou l'iverse :lol3: si tu crois que ce n'ai pas faut dit montre moi comment alors , et merci