JE bloque un ti coup de main merci :)
15 messages
- Page 1 sur 1
JE bloque un ti coup de main merci :)
BONJOUR OU BONSOIR
C'est tout l'exos,qui me pose problème :mur:
1.Démontrer que pour tout réel t strictement positif :
ln(1+t) supérieur t/(1+t)
"dans l'aide il me suggère d'étudier le sens de variation d'une fonction bien choisie puis en déduire son signe."
- j'ai essayer de faire le tableau de signe des 2 fonctions sa m'a pas aidé
2.Soit f la fonction définie pour tout réel x par:
f(x)=e^-x ln(1+e^x)
a.calculer la dérivée de la fonction f.
b.etudier le sens de variation de la fonction f sur R.
c. Calculer lim f(x) quand x tend vers + l'inf et lim f(x) quand x tend vers - l'infinie
donner une interprétation graphique de ces limites.
3.a Pour tout réel x, vérifier que f(x)=1-f'(x)-e^x/(1+e^x)
b.en déduire , en fonction de f , une primitive F de f sur R.
4.Calculer l'intégrale de f entre 0 et 1 .
Mercie pour ceux qui voudrons bien m'aidé .
C'est tout l'exos,qui me pose problème :mur:
1.Démontrer que pour tout réel t strictement positif :
ln(1+t) supérieur t/(1+t)
"dans l'aide il me suggère d'étudier le sens de variation d'une fonction bien choisie puis en déduire son signe."
- j'ai essayer de faire le tableau de signe des 2 fonctions sa m'a pas aidé
2.Soit f la fonction définie pour tout réel x par:
f(x)=e^-x ln(1+e^x)
a.calculer la dérivée de la fonction f.
b.etudier le sens de variation de la fonction f sur R.
c. Calculer lim f(x) quand x tend vers + l'inf et lim f(x) quand x tend vers - l'infinie
donner une interprétation graphique de ces limites.
3.a Pour tout réel x, vérifier que f(x)=1-f'(x)-e^x/(1+e^x)
b.en déduire , en fonction de f , une primitive F de f sur R.
4.Calculer l'intégrale de f entre 0 et 1 .
Mercie pour ceux qui voudrons bien m'aidé .
Salut !
Etudie sur la fonction
la fonction =\frac{t}{1+t}- \ln(1+t)) pour montrer que pour tout
pour montrer que pour tout 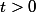 ,
, \ge 0) .
.
malili14 a écrit:(...)
1.Démontrer que pour tout réel t strictement positif :
ln(1+t) supérieur t/(1+t)
"dans l'aide il me suggère d'étudier le sens de variation d'une fonction bien choisie puis en déduire son signe."
- j'ai essayer de faire le tableau de signe des 2 fonctions sa m'a pas aidé
(...)
Etudie sur
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
les limites
je cherche depuis un moment
f(x)=e^-x ln(1+e^x)=1/e^x*ln(1+e^x)
lim qd x tend vers plus l'infinie :1/e^x=0 ,lim ln(1+e^x)=+l'infinie dc forme indéterminée j'ai cherché en factorisant par e^x mais je trouve pas merci de m'aidé
f(x)=e^-x ln(1+e^x)=1/e^x*ln(1+e^x)
lim qd x tend vers plus l'infinie :1/e^x=0 ,lim ln(1+e^x)=+l'infinie dc forme indéterminée j'ai cherché en factorisant par e^x mais je trouve pas merci de m'aidé
lim en - infinie?
je trouve 1/e^x*[x+ln(1+1/e^x)]
pour limite en moins l'infinie ça me pose encore un blème :
lim quand s tend vers -l'infinie, 1/e^x=+l'infinie; lim de [x+ln...] = FI
j'ai factorisé par ln : ln(x/ln+(1+1/e^x) je c pas pr x/ln :help:
pour limite en moins l'infinie ça me pose encore un blème :
lim quand s tend vers -l'infinie, 1/e^x=+l'infinie; lim de [x+ln...] = FI
j'ai factorisé par ln : ln(x/ln+(1+1/e^x) je c pas pr x/ln :help:
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 89 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
