Besoin d'un petit coup de main merci
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
diox
- Membre Naturel
- Messages: 31
- Enregistré le: 22 Oct 2010, 21:17
-
 par diox » 23 Oct 2010, 16:41
par diox » 23 Oct 2010, 16:41
Jimm15 a écrit:Non, il ny a aucune asymptote en

ou en

pour

pour la simple et bonne raison que :
=\sqrt{f(2)}=\sqrt{0}=0)
et
=\sqrt{f(7)}=\sqrt{0}=0)
As-tu étudié les limites de

en -

et en

? Quen déduis-tu ?
g fait lim h (1) vers -inf = 1
etlim h (+infini) vers + infini = +inf
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 23 Oct 2010, 16:59
par Jimm15 » 23 Oct 2010, 16:59
Cest juste mais la rédaction est strictement inacceptable.
On écrit :
=1)
et

Doù
=1)
=+\infty)
et

Doù
=+\infty)
Quen déduit-on pour le comportement asymptotique de

en

et en

?
-
diox
- Membre Naturel
- Messages: 31
- Enregistré le: 22 Oct 2010, 21:17
-
 par diox » 23 Oct 2010, 17:06
par diox » 23 Oct 2010, 17:06
Jimm15 a écrit:Cest juste mais la rédaction est strictement inacceptable.
On écrit :
=1)
et

Doù
=1)
=+\infty)
et

Doù
=+\infty)
Quen déduit-on pour le comportement asymptotique de

en

et en

?
donc pour h il y aurait une assyptote verticale ?
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 23 Oct 2010, 17:08
par Jimm15 » 23 Oct 2010, 17:08
diox a écrit:donc pour h il y aurait une assyptote verticale ?
Non. Cest une asymptote horizontale. Jaimerais que tu me précises léquation de la droite qui est asymptote à la courbe de

et si cest en

ou bien en

?
-
diox
- Membre Naturel
- Messages: 31
- Enregistré le: 22 Oct 2010, 21:17
-
 par diox » 23 Oct 2010, 17:14
par diox » 23 Oct 2010, 17:14
Jimm15 a écrit:Non. Cest une asymptote horizontale. Jaimerais que tu me précises léquation de la droite qui est asymptote à la courbe de

et si cest en

ou bien en

?
dsl je vois pa =P
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 23 Oct 2010, 17:19
par Jimm15 » 23 Oct 2010, 17:19
Lorsque
=b)
, on dit que
la droite déquation 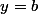 est asymptote horizontale
est asymptote horizontale à la courbe de

en

.
-
diox
- Membre Naturel
- Messages: 31
- Enregistré le: 22 Oct 2010, 21:17
-
 par diox » 23 Oct 2010, 17:27
par diox » 23 Oct 2010, 17:27
Jimm15 a écrit:Lorsque
=b)
, on dit que
la droite déquation 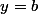 est asymptote horizontale
est asymptote horizontale à la courbe de

en

.
donc je doit mettre assymptote horizontale d'equation y= +infini car lim (+infini )= +infini et lim (1)=1
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 23 Oct 2010, 17:31
par Jimm15 » 23 Oct 2010, 17:31
En

, il ny a aucune asymptote à la courbe de

puisque
=+\infty)
. Cela signifie que
)
peut être rendu « aussi grand que lon veut » dès que

est assez grand.
En

, la droite déquation
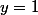
est asymptote horizontale à la courbe de

, daprès la définition énoncée précédemment.
-
diox
- Membre Naturel
- Messages: 31
- Enregistré le: 22 Oct 2010, 21:17
-
 par diox » 23 Oct 2010, 17:44
par diox » 23 Oct 2010, 17:44
Jimm15 a écrit:En

, il ny a aucune asymptote à la courbe de

puisque
=+\infty)
. Cela signifie que
)
peut être rendu « aussi grand que lon veut » dès que

est assez grand.
En

, la droite déquation
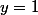
est asymptote horizontale à la courbe de

, daprès la définition énoncée précédemment.
daccord ^^ pour le j j' ai fait lim j(1/1) =1 vers -inf
lim j(1/0) = indefini vers 2 ; lim j(1/0) = indefini vers 7 ; lim j(1/+infini )= 0
-
diox
- Membre Naturel
- Messages: 31
- Enregistré le: 22 Oct 2010, 21:17
-
 par diox » 23 Oct 2010, 18:22
par diox » 23 Oct 2010, 18:22
diox a écrit:daccord ^^ pour le j j' ai fait lim j(1/1) =1 vers -inf
lim j(1/0) = indefini vers 2 ; lim j(1/0) = indefini vers 7 ; lim j(1/+infini )= 0
est ce que ce que j'ai trouvé et correcte ?
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 23 Oct 2010, 18:31
par Jimm15 » 23 Oct 2010, 18:31
-
diox
- Membre Naturel
- Messages: 31
- Enregistré le: 22 Oct 2010, 21:17
-
 par diox » 23 Oct 2010, 18:39
par diox » 23 Oct 2010, 18:39
nan nan ne tinkiete pas je ne rédige pas comme cela sur ma feuille et au faite c cool g trouvé les memes réponses que toi !!

pour l'assymptote de j comment je doit faire ?
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 23 Oct 2010, 18:47
par Jimm15 » 23 Oct 2010, 18:47
Regarde le quatrième message de
CE SUJET.
-
diox
- Membre Naturel
- Messages: 31
- Enregistré le: 22 Oct 2010, 21:17
-
 par diox » 23 Oct 2010, 18:55
par diox » 23 Oct 2010, 18:55
Jimm15 a écrit:Regarde le quatrième message de
CE SUJET.
donc si je comprend bien en -infini assyptote horizzontale ;; en 2 et 7 assymptote verticale ;; en +infini assyptote horizontale
-
diox
- Membre Naturel
- Messages: 31
- Enregistré le: 22 Oct 2010, 21:17
-
 par diox » 23 Oct 2010, 19:09
par diox » 23 Oct 2010, 19:09
diox a écrit:donc si je comprend bien en -infini assyptote horizzontale ;; en 2 et 7 assymptote verticale ;; en +infini assyptote horizontale
ma réponses est elle juste ?
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 24 Oct 2010, 10:44
par Jimm15 » 24 Oct 2010, 10:44
diox a écrit:ma réponses est elle juste ?
Bonjour,
Oui. Rédige correctement sur ta copie.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
ou en
pour
pour la simple et bonne raison que :
et
en -
et en
? Quen déduis-tu ?
, il ny a aucune asymptote à la courbe de
puisque
. Cela signifie que
peut être rendu « aussi grand que lon veut » dès que
est assez grand.
, la droite déquation
est asymptote horizontale à la courbe de
, daprès la définition énoncée précédemment.
en
et
.
en
(car on approche
par valeurs positives daprès le tableau des variations de
) et
.
en
(car on approche
par valeurs négatives daprès le tableau des variations de
) et
.
en
et
.