Exercices d'analyse
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 31 Juil 2006, 19:04
par nox » 31 Juil 2006, 19:04
Oo
perso j'ai vu ca nulle part...
bon bref si vraiment ca te parait pas assez logique alecs20 raisonne comme ca :
sur

la fonction est continue donc admet un minimum sur cet intervalle.
1 : le minimum est en

-> impossible car si

tend vers 0, f(

) tend vers l'infini
2 : le minimum est en

-> impossible car si

tend vers 0, f(

) tend vers l'infini
quelque chose dans ce gout la...
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 31 Juil 2006, 19:13
par Flodelarab » 31 Juil 2006, 19:13
à quoi ça sert de pousser les frontières?
Vous etes pas bien dans l'intervalle de départ ?
En quoi le fait de savoir ce qui se passe en 2 ou 3 (hors de l'intervalle) va vous aidez a traiter de la continuité et de l'existence d'un minimum au milieu ?
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 31 Juil 2006, 19:18
par nox » 31 Juil 2006, 19:18
ca n'est pas pour traiter la continuité...mais si par exemple la limite en 2 était moins l'infini il n'y aurait pas de minimum local...
c'est tout...
-
alecs20
- Membre Relatif
- Messages: 154
- Enregistré le: 16 Jan 2006, 20:14
-
 par alecs20 » 31 Juil 2006, 19:26
par alecs20 » 31 Juil 2006, 19:26
En fait ce devrait etre assez, mais j'intégrais la définition de la limite parce qu'elle serait peut-etre utile pour répondre a la question 2... Prouver l'unicité de ce minimum, c'est une autre paire de manches.
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 31 Juil 2006, 19:27
par Sdec25 » 31 Juil 2006, 19:27
Pour l'unicité du minimum je ne vois pas pourquoi utiliser les limites en 2 et 3.
SI on arrive à montrer que la fonction est décroissante sur un intervalle ouvert ]2,a[, et croissante sur un intervalle ouvert ]b,3[, alors il y a un seul minimum.
Je trouve que tu te complique bien la vie, les 2 premières questions ne demandent pas de rédaction particulièrement longue, et si tu as 1/20 tu te diras que ce n'est pas de ta faute.
-
alecs20
- Membre Relatif
- Messages: 154
- Enregistré le: 16 Jan 2006, 20:14
-
 par alecs20 » 31 Juil 2006, 19:31
par alecs20 » 31 Juil 2006, 19:31
Mais la fonction peut etre décroissante a partir de 2, monter pour faire un maximum, redescendre pour faire un 2e minimym, et devenir croissante en sapprochant de 3. Comment prouver que c'est pas possible.
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 31 Juil 2006, 19:32
par nox » 31 Juil 2006, 19:32
c'est pour la question 2 ca...donc l'unicité...
ba sors les blindés : étudie les variations une fois pour toutes ^^
EDIT : d'ailleurs c'est ce qu'on te demande de faire :D
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 31 Juil 2006, 19:34
par Sdec25 » 31 Juil 2006, 19:34
Pour l'unicité du minimum je ne vois pas pourquoi utiliser les limites en 2 et 3.
Si on arrive à montrer que la fonction est décroissante sur un intervalle ouvert ]2,a[, et croissante sur un intervalle ouvert ]b,3[, alors il y a un seul minimum.
Je trouve que tu te complique bien la vie, les 2 premières questions ne demandent pas de rédaction particulièrement longue, et si tu as 1/20 tu te diras que ce n'est pas de ta faute.
-
alecs20
- Membre Relatif
- Messages: 154
- Enregistré le: 16 Jan 2006, 20:14
-
 par alecs20 » 31 Juil 2006, 19:34
par alecs20 » 31 Juil 2006, 19:34
C'est vrai. Merci:)
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 31 Juil 2006, 19:35
par nox » 31 Juil 2006, 19:35
je suis d'accord avec Sdec25...
faut pas chercher midi à quatorze heure ^^
-
mathelot
 par mathelot » 01 Aoû 2006, 14:22
par mathelot » 01 Aoû 2006, 14:22
Soit

un réel positif quelconque. Comme
=+\infty)
et
=+\infty \quad \exists \alpha > 0)
tel que
 \geq A)
sur le compact

f, continue, atteint un minimum

. Donc

est minimum absolu sur l'ouvert
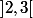
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités