Equations et limites
24 messages
- Page 1 sur 2 - 1, 2
Equations et limites
Bonjour pouvez-vous m'aider à résoudre cet exercice s'il vous plaît?
1. Résoudre dans R:
a) ln racine(2x-2)=ln(4-x)-0.5lnx
b)e^x-2e^(-x)-1=0
c) exp(1+(2/x));)e^x
2.Etudier les limites aux bornes de l'ensemble de définition des fonctions suivantes.
a) f(x)=(2lnx-1)/x. J'ai trouvé que c'était défini sur ]0;+;)[. J'ai trouvé que lim quand x tend vers +;) est 0-.
b) g(x)=exp((x+3)/(x²-1)) Je pense que c'est défini sur R.
c) h(x)=xe^x-e^x+1. Je pense que c'est défini sur R.
d) l(x)=(1/x)-lnx J'ai trouvé que c'était défini sur ]0;+;)[. J'ai trouvé que lim qansd x tend vers +;) est -;).
Merci d'avance pour votre aide.
1. Résoudre dans R:
a) ln racine(2x-2)=ln(4-x)-0.5lnx
b)e^x-2e^(-x)-1=0
c) exp(1+(2/x));)e^x
2.Etudier les limites aux bornes de l'ensemble de définition des fonctions suivantes.
a) f(x)=(2lnx-1)/x. J'ai trouvé que c'était défini sur ]0;+;)[. J'ai trouvé que lim quand x tend vers +;) est 0-.
b) g(x)=exp((x+3)/(x²-1)) Je pense que c'est défini sur R.
c) h(x)=xe^x-e^x+1. Je pense que c'est défini sur R.
d) l(x)=(1/x)-lnx J'ai trouvé que c'était défini sur ]0;+;)[. J'ai trouvé que lim qansd x tend vers +;) est -;).
Merci d'avance pour votre aide.
Serena2095 a écrit:ln(a)+ln(b)=ln(a*b), ln(a)-ln(b)=ln(a/b) et a*ln(b)=ln(b^a) quand a et b sont strictement positifs.
J'ai déja établi ceci mais j ene sais pas si c'est juste:
I.
a) on a: racine(2x-2)=(4-x)/racinex soit racine(2x²-2x)=4-x. Si on élève au carré, on a:2x²-2=x²+8x+16 soit: x²-8x-18=0. On trouve comme solutions: 2+racine136/4 et 2-racine136/4.
b) On a: X-2X^(-1)-1=0 soit X-2/X-1=0
c) je ne vois pas du tout.
II.
a)lim de f quand x tend vers 0 est -;).
b) je ne comprends pas du tout à quoi correspond "exp".
c)je pense qu'en posant e^x=X, on a h(x)=X²-x+1=0 donc on trouve delta négatif donc pas de solutions.
d)lim de l quand x tend vers 0 est +;)
Tu te compliques la vie pour rien, et tu n'as visiblement pas compris comment faire.
Nous avons=\ln(b)) pour a et b strictement positifs, et ce ssi
pour a et b strictement positifs, et ce ssi  (parce que le logarithme népérien est injectif sur
(parce que le logarithme népérien est injectif sur 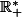 , mais tu n'as pas à savoir ceci).
, mais tu n'as pas à savoir ceci).
Pour la première équation, tu te retrouves avec un logarithme à gauche. A droite se trouve une différence de logarithmes, que tu sais simplifier en un seul logarithme.
Tu pourras donc conclure grâce à ce que je viens de marquer.
Nous avons
Pour la première équation, tu te retrouves avec un logarithme à gauche. A droite se trouve une différence de logarithmes, que tu sais simplifier en un seul logarithme.
Tu pourras donc conclure grâce à ce que je viens de marquer.
Kikoo <3 Bieber a écrit:Tu te compliques la vie pour rien, et tu n'as visiblement pas compris comment faire.
Nous avonspour a et b strictement positifs, et ce ssi
(parce que le logarithme népérien est injectif sur
, mais tu n'as pas à savoir ceci).
Pour la première équation, tu te retrouves avec un logarithme à gauche. A droite se trouve une différence de logarithmes, que tu sais simplifier en un seul logarithme.
Tu pourras donc conclure grâce à ce que je viens de marquer.
Mais j'ai bien compris: pour la a): puisque ln(a)-ln(b)=ln(a/b), on a: ln racine(2x-2)=ln(4-x)-0.5lnx équivaut a ln (racine(2x-2))=ln((4-x)/racinex). donc on a: racine(2x-2)=(4-x)/racinex, non ?
Serena2095 a écrit:Mais j'ai bien compris: pour la a): puisque ln(a)-ln(b)=ln(a/b), on a: ln racine(2x-2)=ln(4-x)-0.5lnx équivaut a ln (racine(2x-2))=ln((4-x)/racinex). donc on a: racine(2x-2)=(4-x)/racinex, non ?
Oui en effet excuse-moi j'ai lu trop vite !
Pour la première mis à part quelques oublis et erreurs, la démarche est bonne.
Serena2095 a écrit:J'ai déja établi ceci mais j ene sais pas si c'est juste:
I.
a) on a: racine(2x-2)=(4-x)/racinex soit racine(2x²-2x)=4-x. Si on élève au carré, on a:2x²-2=x²+8x+16 soit: x²-8x-18=0. On trouve comme solutions: 2+racine136/4 et 2-racine136/4.
En élevant au carré, on obtient 2x²-2x=x²-8x+16
Kikoo <3 Bieber a écrit:Des parenthèses, s'il-te-plait, ce n'est pas très lisible.
Ben o a la b): X-(2/X)-1=0
je pense qu'en mettant au même dénominateur, on a: (X²-2-X)/x=0
soit X²-X-2=0 et a partie de la je trouve deux solutions: -2 et 1.
Mais cela ne correspond pas aux solutions que je trouve à la calculatrice!
Serena2095 a écrit:Ben o a la b): X-(2/X)-1=0
je pense qu'en mettant au même dénominateur, on a: (X²-2-X)/x=0
soit X²-X-2=0 et a partie de la je trouve deux solutions: -2 et 1.
Mais cela ne correspond pas aux solutions que je trouve à la calculatrice!
C'est plutôt -1 et 2 en effet.
Tu as Delta=(-1)²-4(-2)=9 donc deux solutions qui valent respectivement (1-3)/2 et (1+3)/2
[quote="Kikoo <3 Bieber"]Pourquoi -ah pardon c'est moi désolé. Oui dpnc les solutions sont -1 et 2 mais cela ne correspond pas du tout a ce que je trouve a la calculatrice car on a e^(-1) qui vaut environ 0.37 et e^(2) qui vaut 7.39. Hors la courbe ne coupe qu'une fois l'axe des abscisses entre 0 et 1!
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
