Forme explicite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
said_271
- Membre Naturel
- Messages: 17
- Enregistré le: 14 Juil 2006, 15:23
-
 par said_271 » 14 Juil 2006, 21:15
par said_271 » 14 Juil 2006, 21:15
la somme de 0 al'infini des (Pn(x,y)/n!)t expn= (e exp(xt) -1)/(e exp(yt) -1)
peut on avoir une forme explicite des polynome Pn(x,y)
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 14 Juil 2006, 21:31
par nekros » 14 Juil 2006, 21:31
said_271 a écrit:la somme de 0 al'infini des (Pn(x,y)/n!)t expn= (e exp(xt) -1)/(e exp(yt) -1)
peut on avoir une forme explicite des polynome Pn(x,y)
Qu'est-ce qui varie ?
Thomas G :zen:
-
said_271
- Membre Naturel
- Messages: 17
- Enregistré le: 14 Juil 2006, 15:23
-
 par said_271 » 14 Juil 2006, 21:48
par said_271 » 14 Juil 2006, 21:48
nekros a écrit:Qu'est-ce qui varie ?
Thomas G :zen:
les variables réele x,y et t la somme de 0 a l'infenie porte sur n
on a P0(x,y)=x/y
et Pn(x=y,y)-Pn(x,y)= x expn
-
said_271
- Membre Naturel
- Messages: 17
- Enregistré le: 14 Juil 2006, 15:23
-
 par said_271 » 14 Juil 2006, 21:53
par said_271 » 14 Juil 2006, 21:53
said_271 a écrit:les variables réele x,y et t la somme de 0 a l'infenie porte sur n
on a P0(x,y)=x/y
et Pn(x+y,y)-Pn(x,y)= x expn
je veux dire
Pn(x+y,y)-Pn(x,y)= x exp n
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 14 Juil 2006, 21:56
par nekros » 14 Juil 2006, 21:56
C'est bien ça :
}{n!}exp{n}})
?
Thomas G :zen:
-
said_271
- Membre Naturel
- Messages: 17
- Enregistré le: 14 Juil 2006, 15:23
-
 par said_271 » 14 Juil 2006, 22:15
par said_271 » 14 Juil 2006, 22:15
nekros a écrit:C'est bien ça :
}{n!}exp{n}})
?
Thomas G :zen:
sigma de n=0 a l'infini des Pn(x,y) sur n! fois t a la puissance n
P0(x,y)t exp0 tous sur 0!+ (P1(x,y)t exp1 )/1! + (P2(x,y) texp2)2! +........ =
(e a la puissance xt le tous -1)/(e a la puissance yt - 1)
-
Chimomo
- Membre Relatif
- Messages: 275
- Enregistré le: 17 Juin 2006, 09:23
-
 par Chimomo » 14 Juil 2006, 22:20
par Chimomo » 14 Juil 2006, 22:20
Ce serait tellement plus simple si tu utilisais LaTeX.
-
said_271
- Membre Naturel
- Messages: 17
- Enregistré le: 14 Juil 2006, 15:23
-
 par said_271 » 14 Juil 2006, 22:35
par said_271 » 14 Juil 2006, 22:35
Chimomo a écrit:Ce serait tellement plus simple si tu utilisais LaTeX.
je connais pas la forme latex
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 14 Juil 2006, 23:40
par yos » 14 Juil 2006, 23:40

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 14 Juil 2006, 23:49
par nuage » 14 Juil 2006, 23:49
Salut,
yos a écrit: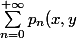\frac{t^n}{n!}=\frac{e^{tx}-1}{e^{ty}-1}})
je veux bien le croire, mais que représente
)
?
C'est une notation que je ne connais pas.
Merci de bien vouloir m'éclairer.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 14 Juil 2006, 23:55
par aviateurpilot » 14 Juil 2006, 23:55
-P_n(x,y)=x^n})
d'apres ce qu'il dit
-
said_271
- Membre Naturel
- Messages: 17
- Enregistré le: 14 Juil 2006, 15:23
-
 par said_271 » 15 Juil 2006, 00:37
par said_271 » 15 Juil 2006, 00:37
yos a écrit: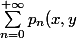\frac{t^n}{n!}=\frac{e^{tx}-1}{e^{ty}-1}})
cé sa
peut on
avoir une forme explicite des polynome Pn(x,y)
-
said_271
- Membre Naturel
- Messages: 17
- Enregistré le: 14 Juil 2006, 15:23
-
 par said_271 » 15 Juil 2006, 00:40
par said_271 » 15 Juil 2006, 00:40
nuage a écrit:Salut,
je veux bien le croire, mais que représente
)
?
C'est une notation que je ne connais pas.
Merci de bien vouloir m'éclairer.
ce sont des polynomes a deux variable x réel qq et y réel non nul
P0(x,y)=x/y
P1(x,y)= xy(x+y)/2*y au carré
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 15 Juil 2006, 00:47
par aviateurpilot » 15 Juil 2006, 00:47
ta question est:
trouver tous le polynomes
)
tel que:
-P_n(x,y)=x^n})
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 15 Juil 2006, 00:53
par aviateurpilot » 15 Juil 2006, 00:53
mais je pense que c'est faux
car si on prend y=0
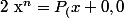-P_n(x,0)=0)
sauf si c'est pas la bonne formule
dit nous la bonne formule+les conditions sur x et y (par exemple : quelque soit x et y de R ......)
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 15 Juil 2006, 09:50
par aviateurpilot » 15 Juil 2006, 09:50
\frac{t^n}{n!}=\frac{e^{ty}-1}{e^{tx}-1}=A)
.
si
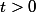
; soit
=e^{tx}-1)
=\frac{ln(x+1)}{t})
j'ai trouvé que.
=P_n(f^{-1}(AB),f^{-1}(B))) quelque
quelque soient (x,y) dans
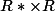
et n dans N.
et il faut prendre B de tel sorte que AB et B soient
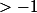
-
said_271
- Membre Naturel
- Messages: 17
- Enregistré le: 14 Juil 2006, 15:23
-
 par said_271 » 15 Juil 2006, 11:20
par said_271 » 15 Juil 2006, 11:20
aviateurpilot a écrit:mais je pense que c'est
car si on prend y=0
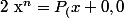-P_n(x,0)=0)
sauf si c'est pas la bonne formule
dit nous la bonne formule+les conditions sur x et y (par exemple : quelque soit x et y de R ......)
y est un réel non nul et x est un réel qq
-
said_271
- Membre Naturel
- Messages: 17
- Enregistré le: 14 Juil 2006, 15:23
-
 par said_271 » 15 Juil 2006, 11:43
par said_271 » 15 Juil 2006, 11:43
aviateurpilot a écrit:\frac{t^n}{n!}=\frac{e^{ty}-1}{e^{tx}-1}=A)
.
si
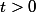
; soit
=e^{tx}-1)
=\frac{ln(x+1)}{t})
j'ai trouvé que.
=P_n(f^{-1}(AB),f^{-1}(B))) quelque
quelque soient (x,y) dans
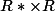
et n dans N.
et il faut prendre B de tel sorte que AB et B soient
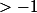
cé pas sa
P0(x,y)=x/y
P1(x,y)= xy(x+y)/2*y au carré
exist il une forme generale explicite des polynomes Pn(x,y)
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 15 Juil 2006, 12:22
par aviateurpilot » 15 Juil 2006, 12:22
said_271 a écrit:cé pas sa
P0(x,y)=x/y
P1(x,y)= xy(x+y)/2*y au carré
exist il une forme generale explicite des polynomes Pn(x,y)
j'ai pas dit le contraire
par exemple pour
=x/y)
si t>0
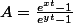
,f^{-1}(B))=ln(AB+1)/ln(B+1))
si on prend
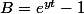
/t=y)
et
/t=ln(A=\frac{e^{xt}-1}{e^{yt}-1}\times e^{yt}-1)=x)
donc
,f^{-1}(B))=ln(AB+1)/ln(B+1)=\frac{ln(AB+1)/t}{Ln(B+1)/t}=x/y}) donc ma formule est vrai
donc ma formule est vrai
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
