Equa diff non linéaire
Olympiades mathématiques, énigmes et défis
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 26 Mai 2012, 22:12
par Zweig » 26 Mai 2012, 22:12
Salut,
Un classique laissé à l'attention des Bac + 1 !
Déterminer toutes les fonctions de classe

vérifiant :
 = f(x))
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 27 Mai 2012, 04:52
par Dinozzo13 » 27 Mai 2012, 04:52
Salut !
Sympa ton défi :++:
Après quelque brève recherche, je suis arrivé à la conclusion que

devait vérifier :

.
Mais pour l'instant, j'arrive pas à résoudre cette équation différentielle :--:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 27 Mai 2012, 11:12
par Zweig » 27 Mai 2012, 11:12
C'est en effet la bonne méthode. Je te laisse réfléchir pour résoudre cette équa diff.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 27 Mai 2012, 11:49
par Dinozzo13 » 27 Mai 2012, 11:49
Zweig a écrit:C'est en effet la bonne méthode.
Alors je suis content d'en être arriver là :+++:
Mais justement, je cale sur sa résolution.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 27 Mai 2012, 11:58
par Zweig » 27 Mai 2012, 11:58
Une petite piste : il y aura un changement de variables à faire. Inspire-toi de la résolution des équa diff linéaires de degré 2, en particulier, la méthode pour obtenir l'équation caractéristique.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 27 Mai 2012, 12:03
par Dinozzo13 » 27 Mai 2012, 12:03
Pour ce genre d'équation, on est censé effectuer un changement de variable avec du ln mais là je vois vraiment pas.
Les coefficients étant non constants, je vais pas résoudre

?
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 27 Mai 2012, 12:18
par Zweig » 27 Mai 2012, 12:18
Dinozzo13 a écrit:Pour ce genre d'équation, on est censé effectuer un changement de variable avec du ln mais là je vois vraiment pas.
Les coefficients étant non constants, je vais pas résoudre

?
Pas vraiment. L'idée est, avec un changement de variable, de se ramener à une équation différentiel du second ordre à coefficients constants, que tu sais résoudre.
On suppose x > 0 (le cas x < 0 se traite d'une manière analogue). On pose

et
 = \phi(t))
. Il s'agit alors de montrer que

vérifie une équa diff du second ordre à coefficients constants.

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 27 Mai 2012, 12:29
par Olympus » 27 Mai 2012, 12:29
Salut !
Tu peux restreindre le domaine de travail sur

et remarquer [url=http://texify.com/?$\Large \left( y\left( e^t \right) \right)'' - \left( y \left( e^t \right) \right)'=e^{2t} y'' \left( e^t \right)$]ceci[/url] ( lien extérieur au cas où tu ne souhaiterais pas être spoilé Dino :we: )
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 27 Mai 2012, 12:57
par Dinozzo13 » 27 Mai 2012, 12:57
Zweig a écrit:Pas vraiment. L'idée est, avec un changement de variable, de se ramener à une équation différentiel du second ordre à coefficients constants, que tu sais résoudre.
On suppose x > 0 (le cas x < 0 se traite d'une manière analogue). On pose

et
 = \phi(t))
. Il s'agit alors de montrer que

vérifie une équa diff du second ordre à coefficients constants.
Ah ! Punaise, en plus, c'est écrit noir sur blanc dans mon bouquin de mpsi :marteau:
Olympus a écrit:Salut !
( lien extérieur au cas où tu ne souhaiterais pas être spoilé Dino :we: )
Pratique, merci :++:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 27 Mai 2012, 13:04
par Zweig » 27 Mai 2012, 13:04
Dinozzo13 a écrit:Ah ! Punaise, en plus, c'est écrit noir sur blanc dans mon bouquin de mpsi :marteau:
Pratique, merci :++:
Du coup, quelle équation vérifie

?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 27 Mai 2012, 13:09
par Dinozzo13 » 27 Mai 2012, 13:09
excuse-moi, je n'avais pas vu que tu avais répondu.
Donc

vérifie

-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 27 Mai 2012, 13:16
par Zweig » 27 Mai 2012, 13:16
Dinozzo13 a écrit:excuse-moi, je n'avais pas vu que tu avais répondu.
Donc

vérifie

Non, je veux une équation à coefficients constants, là t'es pas plus avancé avec le terme en exp, qui n'est pas constant ...
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 27 Mai 2012, 13:27
par Dinozzo13 » 27 Mai 2012, 13:27
Zweig a écrit:là t'es pas plus avancé avec le terme en exp, qui n'est pas constant ...
oui, c'est pas faux.
Je trouve que

doit vérifier

, ai-je bon ,
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 27 Mai 2012, 13:33
par Zweig » 27 Mai 2012, 13:33
Oui :lol3:
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 27 Mai 2012, 13:40
par Dinozzo13 » 27 Mai 2012, 13:40
Ben du coup c'est fini !
je résous

donc

ou

.
Par contre ce qui m'embête, c'est que je ne sais jamais quelle formule mettre pour la solution générale vue que j'en ai vu plusieurs !
Je mettrai
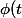=\lambda e \sqrt 2 e^{i \frac{\pi}{3}t} +\mu \sqrt 2 e^{-i \frac{\pi}{3}t})
avec

.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 27 Mai 2012, 13:56
par Zweig » 27 Mai 2012, 13:56
Eh bien, si tu as deux solutions complexes (qui sont conjuguées,

) alors les solutions sont données par
 = e^{ax}(A\cos\,bx + B\sin\,bx))
ou
 = Qe^{ax}\cos\,(bx + R))
Ne pas oublier qu'ici, c'est
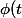)
qui est solution est que

-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 27 Mai 2012, 21:16
par Dinozzo13 » 27 Mai 2012, 21:16
Zweig a écrit:Pas vraiment. L'idée est, avec un changement de variable, de se ramener à une équation différentiel du second ordre à coefficients constants, que tu sais résoudre.
(...) On pose

et
 = \phi(t))
. Il s'agit alors de montrer que

vérifie une équa diff du second ordre à coefficients constants.
Une question me trotte : pourquoi avoir poser
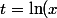)
?
Qu'est-ce qui t'a aiguillé vers ce changement de variable ?
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 27 Mai 2012, 21:28
par Zweig » 27 Mai 2012, 21:28
Je pose
 = g(t))
avec
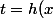)
.
Alors,
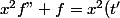^2g"(t) + x^2t"g'(t) + g(t))
On cherche t de sorte que les coefficients de l'expression de droite soient constants. En particulier, on cherche t de sorte que
^2 = K)
, soit

, donc

.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 27 Mai 2012, 22:15
par Dinozzo13 » 27 Mai 2012, 22:15
J'allais oublier, il faut montrer également que f est de deux fois dérivable non ?

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 27 Mai 2012, 22:26
par Olympus » 27 Mai 2012, 22:26
Dinozzo13 a écrit:J'allais oublier, il faut montrer également que f est de deux fois dérivable non ?
L'équation justement te dit que si
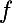
est de classe
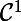
, alors il en est de même pour
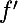
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
?
et
. Il s'agit alors de montrer que
vérifie une équa diff du second ordre à coefficients constants.
et
. Il s'agit alors de montrer que
vérifie une équa diff du second ordre à coefficients constants.