Suite non linéaire.
Olympiades mathématiques, énigmes et défis
-
un_homme
- Membre Naturel
- Messages: 89
- Enregistré le: 06 Nov 2008, 18:54
-
 par un_homme » 06 Avr 2015, 12:24
par un_homme » 06 Avr 2015, 12:24
Salut,
On considère la suite
+2)
Calculer

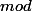

avec
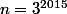
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 06 Avr 2015, 12:45
par Doraki » 06 Avr 2015, 12:45
C'est U(n-2) ou (Un)-2 ?
Et U0 vaut combien ?
-
un_homme
- Membre Naturel
- Messages: 89
- Enregistré le: 06 Nov 2008, 18:54
-
 par un_homme » 06 Avr 2015, 13:28
par un_homme » 06 Avr 2015, 13:28
En fait, on peut exprimer

en fonction de

,

et des fonction usuelles.
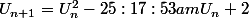

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Avr 2015, 13:57
par Ben314 » 06 Avr 2015, 13:57
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Avr 2015, 14:42
par Ben314 » 06 Avr 2015, 14:42
Un soupons (sic) plus compliqué :
Peut tu me donner
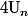
en fonction de

et de
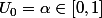
dans le cas où
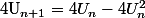
?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
un_homme
- Membre Naturel
- Messages: 89
- Enregistré le: 06 Nov 2008, 18:54
-
 par un_homme » 08 Avr 2015, 05:23
par un_homme » 08 Avr 2015, 05:23
Salut,
J'ai trouvé pour

on prend

tel que
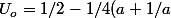)
alors
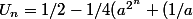^{2^n}))
-
un_homme
- Membre Naturel
- Messages: 89
- Enregistré le: 06 Nov 2008, 18:54
-
 par un_homme » 08 Avr 2015, 06:05
par un_homme » 08 Avr 2015, 06:05
En prenant a complexe sur le cercle unité, on l'obtient pour n'importe quel

entre 0 et 1.
Pour la réponse
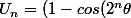)/2)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 08 Avr 2015, 09:19
par Ben314 » 08 Avr 2015, 09:19
un_homme a écrit:En prenant a complexe sur le cercle unité, on l'obtient pour n'importe quel

entre 0 et 1.
Pour la réponse
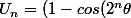)/2)
:king2:

Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 08 Avr 2015, 11:44
par Ben314 » 08 Avr 2015, 11:44
Remarque :
Une fois qu'on a conjecturé le résultat (et ç'est là que c'est pas gagné...), la preuve est "triviale" du fait que :
=\big(2\sin(\theta)\cos(\theta)\big)^2=4\sin^2(\theta)(1-\sin^2(\theta)))
Donc la suite
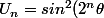)
vérifie
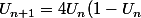)
Donc, pour répondre exactement à la question de départ, on a
\big)\ \ \ \)
:hein:
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
un_homme
- Membre Naturel
- Messages: 89
- Enregistré le: 06 Nov 2008, 18:54
-
 par un_homme » 08 Avr 2015, 13:31
par un_homme » 08 Avr 2015, 13:31
Je suis partie sur une forme algébrique, que j'ai trouvé mais en galérant bien (à noter quel marche pour

)
Aller je m'auto-défie : trouver l'expression générale de

en fonction de

tel que :
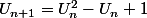
.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 08 Avr 2015, 15:05
par Ben314 » 08 Avr 2015, 15:05
Je ne sais pas, dans ce cas là, exprimer Un en fonction de n et U0 à l'aide des fonctions "élémentaires"...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 08 Avr 2015, 19:31
par zygomatique » 08 Avr 2015, 19:31
salut
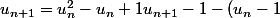 = (u_n - 1)^2)
on effectue le changement de variable
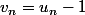
et on obtient ::
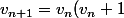 \\<br />v_n = v_{n - 1}(v_{n - 1} + 1) \\<br />... \\<br />v_2 = v_1(v_1 + 1) \\<br />v_1 = v_0(v_0 + 1))
soit en multipliant membre à membre et avec les bonnes conditions

on obtient que ::
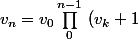)
mais ensuite ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
un_homme
- Membre Naturel
- Messages: 89
- Enregistré le: 06 Nov 2008, 18:54
-
 par un_homme » 08 Avr 2015, 20:11
par un_homme » 08 Avr 2015, 20:11
Salut,
Pour ma part je partirais plus tôt vers, la recherche de suite

exprimer explicitement et qui permet de déterminer une relation du type du type :
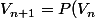)
avec P un polynôme de degré 2.
il y a déjà :
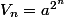
et

Mais elle n'aide pas dans ce cas, et je cherche donc d'autres formes.
Je prend le problème à l'envers.
Remarque : si on trouve
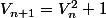
c'est gagné.
)
soit

homographie on regarde
=f(Q(f^{-1}(x))))
Si l'on sait calculer
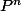
alors on sait calculer
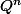
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités