[BAC +1] Equa diff non linéaire II
Olympiades mathématiques, énigmes et défis
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 27 Mai 2012, 19:22
par Zweig » 27 Mai 2012, 19:22
Salut,
Déterminer toutes les fonctions réelles vérifiant :
i)
^2}y=0)
ii)

(équations indépendantes)
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 27 Mai 2012, 19:46
par Zweig » 27 Mai 2012, 19:46
Cette fois-ci, je ne donne plus d'indices, à vous Bac + 1 de vous débrouiller par vous-même (cela dit, la méthode à utiliser est similaire à l'exercice précédent, reste à savoir quel t prendre)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 27 Mai 2012, 22:50
par Dinozzo13 » 27 Mai 2012, 22:50
Salut !
Moi qui adorent les équations différentielles, tu me gâtes ^^
Première je sais que l'on doit effectuer le changement de variable
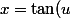)
, mais je n'arrive pas à le prouver.
Je te montre comment j'ai commencer :++:
Je pose
=g(t))
avec
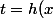)
.
=t'g'(t))
;
=t''g'(t)+\(t'\)^2g''(t))
donc
^2}y=0)
équivaut à
+\(t'\)^2g''(t)+\frac{2x}{x^2+1}t'g'(t)+ \frac{1}{(x^2+1)^2} g(t)=0)
^2g''(t)+\(t''+\frac{2x}{x^2+1}t'\)g'(t)+ \frac{1}{(x^2+1)^2} g(t)=0)
^2\(t'\)^2 g''(t) + \( x^2+1 t''+2x t' \)(x^2+1) g'(t)+ g(t)=0)
Déterminons alors

tel que
^2\(t'\)^2)
et
(x^2+1))
soient des constantes.
Soit

une constante.
^2\(t'\)^2=K)
donc
^2=\frac{K}{x^2+1})

avec

Mais après je sèche.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 27 Mai 2012, 23:35
par Zweig » 27 Mai 2012, 23:35
C'est normal que tu sèches, c'est plutot t' = K'/(x^2 + 1) :lol3:
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 28 Mai 2012, 06:08
par Dinozzo13 » 28 Mai 2012, 06:08
Zweig a écrit:C'est normal que tu sèches, c'est plutot t' = K'/(x^2 + 1) :lol3:
Oulà oui, merci :++:
Dinozzo13 a écrit:(...)
^2\(t'\)^2=K)
donc
^2=\frac{K}{x^2+1})

avec

Mais après je sèche.
C'est vrai que lorsqu'on y regarde de plus près, c'est n'importe quoi !
Si je ne me suis pas trompé, je trouve, pour la première :
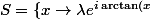} +\mu e^{-i \arctan(x)} | (\lambda,\mu)\in\mathbb{C}^2 \})
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 28 Mai 2012, 07:17
par Dinozzo13 » 28 Mai 2012, 07:17
Pour la deuxième, je trouve :
\in\mathbb{R}^2 \right})
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 28 Mai 2012, 11:17
par Zweig » 28 Mai 2012, 11:17
Dinozzo13 a écrit:Oulà oui, merci :++:
C'est vrai que lorsqu'on y regarde de plus près, c'est n'importe quoi !
Si je ne me suis pas trompé, je trouve, pour la première :
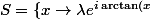} +\mu e^{-i \arctan(x)} | (\lambda,\mu)\in\mathbb{C}^2 \})
Tu pourrais modifier ça histoire de faire dégager les "i" (en exprimant ça sous la forme
)
avec

les racines conjuguées.)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 28 Mai 2012, 19:46
par Dinozzo13 » 28 Mai 2012, 19:46
} +\mu e^{-i \arctan(x)})
} + e^{-i \arctan(x)} \)+(\mu-\lambda) e^{-i \arctan(x)})
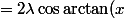 \) +(\mu - \lambda) e^{-i \arctan(x)})
.
Mais je vois pas bien comment faire pour obtenir la même formule que toi.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 28 Mai 2012, 21:08
par Zweig » 28 Mai 2012, 21:08
Salut,
Bah suffit de prendre la partie réelle de f (tu as un lemme dans ton cours qui montre que f solution complexe de l'équation homogène => Re f aussi solution, si l'équation homogène a tous ses coefficients réels.)
Si ton déterminant est négatif, les solutions de l'équation caractéristique sont

. Du coup,
 = (A + iB)e^{(a+ib)x} + (A'+iB')e^{(a-ib)x} = e^{ax}((A+ib)e^{ibx} + (A'+iB')e^{-ibx}))
Puis tu passes à la partie réelle et remarque que
)
et
^2 + \left(\frac{v}{\sqrt{u^2+v^2}}\right)^2 = 1)
,
donc il existe un réel

dans
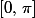
vérifiant :

et

EDIT : Bon, faut bien sûr remplacer dans ton cas x par arctan x ..
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 28 Mai 2012, 21:21
par Dinozzo13 » 28 Mai 2012, 21:21
:doh: pourquoi faire tout ça ?
Ne peut-on pas garder la fonction sous la forme d'une somme de deux exponentielles complexes ?
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 28 Mai 2012, 21:51
par Zweig » 28 Mai 2012, 21:51
Bah f est supposée une fonction de R dans R. Si tu la gardes telle quelle, tu auras une fonction complexe ...
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 28 Mai 2012, 22:03
par Dinozzo13 » 28 Mai 2012, 22:03
Ah mince alors !
Bon, je vais voir ça alors :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités