1èreS - Exercie Suite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
cr@sh
- Messages: 9
- Enregistré le: 20 Mai 2012, 15:17
-
 par cr@sh » 20 Mai 2012, 15:46
par cr@sh » 20 Mai 2012, 15:46
Bonjour,
Je suis coincé dans un exercice sur les suites, j'aimerais si possible avoir une aide pour continuer. :hein:
Je vous le met en page:

Pour la question
1. j'ai trouvé:
u2 = 1
u3 = 2
u4 = 3
u5 = 5
Pour la question
2. j'ai trouvé:
alpha = [1 - rac(5)] / 2
beta = [1 + rac(5)] / 2
Voilà, je bloque à la question
3. , et la question
4. me parait dans le même style >.<
Pouvez-vous m'aider?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 20 Mai 2012, 15:47
par Dinozzo13 » 20 Mai 2012, 15:47
Salut !
Rien n'est affiché
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 20 Mai 2012, 15:51
par Dinozzo13 » 20 Mai 2012, 15:51
Salut !
3. Montre que
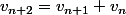
avec
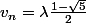^n + \mu \( \frac{1 + \sqrt 5}{2}\)^n)
:+++:
4.
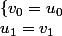
équivaut à
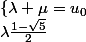 + \mu \( \frac{1 + \sqrt 5}{2}\)=u_1)
:+++:
-
cr@sh
- Messages: 9
- Enregistré le: 20 Mai 2012, 15:17
-
 par cr@sh » 20 Mai 2012, 16:29
par cr@sh » 20 Mai 2012, 16:29
merci de ton aide!
je ne cache pas que je galère x)
-
cr@sh
- Messages: 9
- Enregistré le: 20 Mai 2012, 15:17
-
 par cr@sh » 20 Mai 2012, 18:28
par cr@sh » 20 Mai 2012, 18:28
ouf! J'ai réussi les questions 3 et 4 ^^
Mais j'ai un nouveau probleme... à la question 5, je ne trouve rien... :doh:
I need help :x
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 20 Mai 2012, 18:56
par nodjim » 20 Mai 2012, 18:56
Pour la 5, c'est la sommation de termes identiques à puissances incrémentées algébriquement, ça devrait te rappeler quelque chose...
-
cr@sh
- Messages: 9
- Enregistré le: 20 Mai 2012, 15:17
-
 par cr@sh » 20 Mai 2012, 19:47
par cr@sh » 20 Mai 2012, 19:47
euh... O_O
-
cr@sh
- Messages: 9
- Enregistré le: 20 Mai 2012, 15:17
-
 par cr@sh » 20 Mai 2012, 20:17
par cr@sh » 20 Mai 2012, 20:17
vraiment, j'y arrive pas... :(
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 20 Mai 2012, 20:21
par Kikoo <3 Bieber » 20 Mai 2012, 20:21
nodjim a écrit:Pour la 5, c'est la sommation de termes identiques à puissances incrémentées algébriquement, ça devrait te rappeler quelque chose...
Mouahahahahaahahahah ! :ptdr: (et toi qui disais "Kikoo: niveau 5ème..." !!)
Sinon, quelles valeurs as-tu trouvé pour

et

?
-
cr@sh
- Messages: 9
- Enregistré le: 20 Mai 2012, 15:17
-
 par cr@sh » 20 Mai 2012, 20:23
par cr@sh » 20 Mai 2012, 20:23
alpha = [1 - rac(5)] / 2
beta = [1 + rac(5)] / 2
-
cr@sh
- Messages: 9
- Enregistré le: 20 Mai 2012, 15:17
-
 par cr@sh » 20 Mai 2012, 20:29
par cr@sh » 20 Mai 2012, 20:29
et j'ai aussi trouvé:
lambda = - 1 / racine(5)
mu = 1 / racine(5)
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 20 Mai 2012, 20:32
par Kikoo <3 Bieber » 20 Mai 2012, 20:32
Okei !

On pose tout d'abord
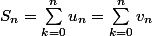
Cela donne directement
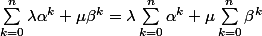
par linéarité de l'addition.
Ensuite, à toi de te débrouiller !

J'avais oublié de corriger ici aussi ^^
-
cr@sh
- Messages: 9
- Enregistré le: 20 Mai 2012, 15:17
-
 par cr@sh » 20 Mai 2012, 20:46
par cr@sh » 20 Mai 2012, 20:46
merci mais là ça m'énerve
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 20 Mai 2012, 20:55
par Kikoo <3 Bieber » 20 Mai 2012, 20:55
Ok, je t'avoue que le calcul est un peu long en effet !
rapidement, on remplace par les valeurs alpha, bêta, et caetera...
C'la fait :
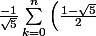^k+\frac{1}{\sqrt{5}}\sum_{k=0}^n \left(\frac{1+\sqrt{5}}{2}\right)^k)
^n-1}{\frac{1-\sqrt{5}}{2}-1}+\frac{1}{\sqrt{5}}\frac{\left(\frac{1+\sqrt{5}}{2}\right)^n-1}{\frac{1+\sqrt{5}}{2}-1}=...)
^n-1}{\sqrt{5}+1}+\frac{2}{\sqrt{5}}\frac{\left(\frac{1+\sqrt{5}}{2}\right)^n-1}{\sqrt{5}-1})
^n-1}{\sqrt{5}+1}+\frac{\left(\frac{1+\sqrt{5}}{2} \right)^n-1}{\sqrt{5}-1} \right))
Si je me suis pas trompé...
Et normalement, je trouve -1 pour la limite de ce machin...
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 20 Mai 2012, 20:59
par Dinozzo13 » 20 Mai 2012, 20:59
la première ligne, ce sont des "k" en exposant
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 20 Mai 2012, 21:00
par Kikoo <3 Bieber » 20 Mai 2012, 21:00
Dinozzo13 a écrit:la première ligne, ce sont des "k" en exposant
Merci beaucoup !

-
cr@sh
- Messages: 9
- Enregistré le: 20 Mai 2012, 15:17
-
 par cr@sh » 20 Mai 2012, 21:29
par cr@sh » 20 Mai 2012, 21:29
merci!
les "k exposants" sont pris au hasard ou c'est parce que en dessous de sum y a k=0 ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 20 Mai 2012, 22:01
par Dinozzo13 » 20 Mai 2012, 22:01
cr@sh a écrit:merci!
les "k exposants" sont pris au hasard ou c'est parce que en dessous de sum y a k=0 ?
Tout à fait :++:
Si on avait eu i=..., il y aurait eu i
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 84 invités

