Bonjour !
Comment calculer le rayon de convergence de la série entière de terme général ;)an z^n
avec an=tan(n*Pi/7)
Merci
Rayon de convergence / série entière
5 messages
- Page 1 sur 1
mathelot a écrit:bonjour,
sauf erreur, le critère de Cauchy est= limsup
la suite des tangentes ne prend qu'au plus 7 valeurs, ça devrait donner R=1 et la possibilité de calculer explicitement la somme (modulo 7)
Pouvez vous détaillez plus, s'il vous plait ? On vient de commencer le chapitre, je ne comprends pas trop la réponse :mur:
Mercii
Bonjour,
pour une suite réelle) bornée
bornée
on remarque que est
est
- décroissante, minorée, convergente
on note
 = \lim_{n} \, (\sup_{k \geq n} v_k))
pour tout , à partir d'un certain rang
, à partir d'un certain rang

car les "sup" passant sous , les termes de la suite
, les termes de la suite ) aussi
aussi
Quand on applique la notion de "limsup" aux séries entières
^n |z|^n)
à partir d'un certain rang si
on voit alors que pour les z vérifiant
 \frac{1}{L+\epsilon})
donc
de même, l'inégalité

maintenant la suite|) est 7-périodique, la limsup de
est 7-périodique, la limsup de  est donc 1.
est donc 1.
(toutes proportions gardées, c'est comme si tu considérais)
pour une suite réelle
on remarque que
- décroissante, minorée, convergente
on note
pour tout
car les "sup" passant sous
Quand on applique la notion de "limsup" aux séries entières
à partir d'un certain rang si
on voit alors que pour les z vérifiant
donc
de même, l'inégalité
maintenant la suite
(toutes proportions gardées, c'est comme si tu considérais
Salut,
Les programmes actuels de prépa ne prévoient pas la formule de Hadamard.
Il est simple de démontrer que si) est une suite non nulle à ensemble de valeurs fini alors le rayon de convergence de la série entière
est une suite non nulle à ensemble de valeurs fini alors le rayon de convergence de la série entière 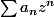 est égal à
est égal à  .
.
En effet : comme la suite) est bornée on a déjà
est bornée on a déjà 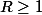
Soit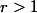 alors si
alors si  (
( existe et
existe et  car les hypothéses disent que la suite est finie et non nulle ) on a bien :
car les hypothéses disent que la suite est finie et non nulle ) on a bien :  lorsque
lorsque 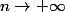 , par suite
, par suite 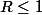
Remarque1 : une conséquence de cela est : si la suite) est périodique non nulle alors le rayon de convergence de la série entièer
est périodique non nulle alors le rayon de convergence de la série entièer 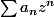 est égal à
est égal à 
Remarque 2 : Si) est une suite convergnete de limite non nulle alors là aussi : le rayon de convergence de la série entièer
est une suite convergnete de limite non nulle alors là aussi : le rayon de convergence de la série entièer 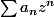 est égal à
est égal à 
.
Les programmes actuels de prépa ne prévoient pas la formule de Hadamard.
Il est simple de démontrer que si
En effet : comme la suite
Soit
Remarque1 : une conséquence de cela est : si la suite
Remarque 2 : Si
.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 169 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
