Rayon de convergence série entière

[alben]

Bonsoir,

J'ai l'impression de ne plus rien comprendre. Quelque chose de très simple m'échappe !
On a la fonction de C dans C.
est défini comme le plus grand des coefs dans le développement de .
Lorsqu'on développe ces termes, on constate qu'il n'y a pas de recoupement entre les puissances de z, que l'on peut écrire où les sont égaux à [list]
[*]0 si

[alben]

Bonjour,

Je me permet de remonter cette question qui s'est enterrée un peu trop vite :hein:

[yos]

Salut Alben.
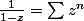
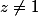
A première vue je dirais que c'est un peu comme l'égalité , où le premier membre est défini pour , et le second membre pour .
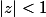
Donc pas trop surprenant.
Je vais regarder de plus près.

[alben]

Bonjour et merci Yos,
Et oui c'est bien ça, j'ai des termes qui deviennent infinis lorsque |z|>1 (ceux dont les coeff sont égaux à 1) et ce n'est qu'en regroupant que l'on trouve des paquets dont les sommes sont convergentes.
Ce qui m'a perturbé, c'est que le développement des z(1-z) ne regroupe ni ne commute de termes...

[yos]

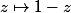
Oui c'est quand même assez troublant. Vue que f est stable par notamment.

Ce qui m'a perturbé, c'est que le développement des z(1-z) ne regroupe ni ne commute de termes...

Ceci ne devrait pas intervenir je crois : la convergence dans le disque est absolue donc commutative.