Nombre complexe.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
dr.dre
- Membre Naturel
- Messages: 76
- Enregistré le: 27 Oct 2011, 18:49
-
 par dr.dre » 04 Déc 2011, 18:22
par dr.dre » 04 Déc 2011, 18:22
Bonjour,
Soit
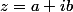
(forme algébrique). Il faut exprimer le module des nombres complexes :
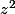
: j'ai trouvé


: j'ai trouvé

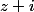
: j'ai trouvé

\times(2z-1))
/ la je trouve

... Faut il que je factorise ?
Est-ce-que le reste est juste ?
Merci de votre aide !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Déc 2011, 18:33
par Nightmare » 04 Déc 2011, 18:33
Salut,
es-tu sûr de répondre à la bonne question?
Qu'as-tu calculé pour obtenir a²+2aib+b² par exemple? Que te demande-t-on de calculer?
-
dr.dre
- Membre Naturel
- Messages: 76
- Enregistré le: 27 Oct 2011, 18:49
-
 par dr.dre » 04 Déc 2011, 18:43
par dr.dre » 04 Déc 2011, 18:43
Il faut trouver le module. Le module de
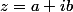
c'est

. Mais je sais pas en fait je suis perdu..
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Déc 2011, 18:44
par Nightmare » 04 Déc 2011, 18:44
Et donc? Quel est le rapport avec tes résultats?
-
dr.dre
- Membre Naturel
- Messages: 76
- Enregistré le: 27 Oct 2011, 18:49
-
 par dr.dre » 04 Déc 2011, 18:48
par dr.dre » 04 Déc 2011, 18:48
En fait moi j'ai fais par exemple pour le le Z² j'ai mis a+ib au carré mais c'est pas ça qu'il faut faire .
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Déc 2011, 18:50
par Nightmare » 04 Déc 2011, 18:50
Tu calcules donc z². Mais ce n'est pas z² que l'on veut mais son module. Que faire ensuite?
-
dr.dre
- Membre Naturel
- Messages: 76
- Enregistré le: 27 Oct 2011, 18:49
-
 par dr.dre » 04 Déc 2011, 19:00
par dr.dre » 04 Déc 2011, 19:00
Moi je dirai que module de Z²=
^2+(2aib)^2})
..
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Déc 2011, 19:02
par Nightmare » 04 Déc 2011, 19:02
C'est presque ça, mais d'où vient le (2aib)² ?
-
dr.dre
- Membre Naturel
- Messages: 76
- Enregistré le: 27 Oct 2011, 18:49
-
 par dr.dre » 04 Déc 2011, 19:05
par dr.dre » 04 Déc 2011, 19:05
Ah c'est (2ab)² c'est ça ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Déc 2011, 19:06
par Nightmare » 04 Déc 2011, 19:06
Tout à fait!
Tu peux essayer de réduire l'expression sous la racine, même si ce n'est pas essentiel.
-
dr.dre
- Membre Naturel
- Messages: 76
- Enregistré le: 27 Oct 2011, 18:49
-
 par dr.dre » 04 Déc 2011, 19:15
par dr.dre » 04 Déc 2011, 19:15
Je n'écris pas les calculs mais cela me donne a²+b². C'est juste ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Déc 2011, 19:21
par Nightmare » 04 Déc 2011, 19:21
Comment obtiens-tu ça?
-
dr.dre
- Membre Naturel
- Messages: 76
- Enregistré le: 27 Oct 2011, 18:49
-
 par dr.dre » 04 Déc 2011, 19:26
par dr.dre » 04 Déc 2011, 19:26
|a²+2iab-b²|
=rac((a²-b²)²+(2ab)²)
=rac((a^4-2a²b²+b^4)+4a²b²)
=rac(a^4+2a²b²+b^4)
=rac((a²+b²)²)
=a²+b²
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Déc 2011, 19:29
par Nightmare » 04 Déc 2011, 19:29
C'est ok.
Ne vois-tu pas une propriété du module qui nous aurait permis d'avoir ce résultat beaucoup plus rapidement?
Plus précisément, il y a-t-il un lien entre |z| et |z²| ?
-
dr.dre
- Membre Naturel
- Messages: 76
- Enregistré le: 27 Oct 2011, 18:49
-
 par dr.dre » 04 Déc 2011, 19:31
par dr.dre » 04 Déc 2011, 19:31
|z|=

|z²|=
^2})
= a²+b² ? ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Déc 2011, 19:35
par Nightmare » 04 Déc 2011, 19:35
Hum, d'où vient ceci : |z²|=sqrt((a²+b²)²)? Quelle formule as-tu utilisé?
-
dr.dre
- Membre Naturel
- Messages: 76
- Enregistré le: 27 Oct 2011, 18:49
-
 par dr.dre » 04 Déc 2011, 19:43
par dr.dre » 04 Déc 2011, 19:43
Aucune ça parait logique pour moi x)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Déc 2011, 19:46
par Nightmare » 04 Déc 2011, 19:46
Pourquoi le serait-ce? Il s'avère que c'est vrai par pure coïncidence, mais ça ne vient d'aucune formule a priori.
Connais-tu des propriétés du module?
Par exemple, |z*z'|=|z|*|z'| ?
-
dr.dre
- Membre Naturel
- Messages: 76
- Enregistré le: 27 Oct 2011, 18:49
-
 par dr.dre » 04 Déc 2011, 20:08
par dr.dre » 04 Déc 2011, 20:08
Oui il y a aussi l'inégalité triangulaire par exemple. Mais je ne comprends pas vraiment que représente z'. C'est la dérivé de Z ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Déc 2011, 20:10
par Nightmare » 04 Déc 2011, 20:10
Non non, c'est juste une notation pour désigner un autre complexe que z.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités