Topologie et continuité sur un evn!

[Exquise Sensation]

Soit E=R^n, f:E->E telle que pour tout (z,z')dans E² f(z+z')=f(z)+f(z')

et pour tout q rationnel et z élément de E, f(qz)=qf(z).
on suppose de plus (soyons fou!) que f est bornée sur une partie de E d'intérieur non vide.

Montrer que f est R-linéaire.

[Anonyme]

Soit E=R^n, f:E->E telle que pour tout (z,z')dans E² f(z+z')=f(z)+f(z')

et pour tout q rationnel et z élément de E, f(qz)=qf(z).
on suppose de plus (soyons fou!) que f est bornée sur une partie de E d'intérieur non vide.

Montrer que cette fonction f est R-linéaire.

Bonjour
Pour montrer que cette fonction f est une fonction R-linéaire il suffit de démontrer que pour tout z de R^n et pour tout k de R on on f(k(z))=kf(z)

Comme on a f(qz)=qf(z) avec q appartenant à Q ,
en utilisant en autre le fait que l'ensemble Q est dense dans l'ensemble R , tu devrais pouvoir démontrer que f(kz)=kf(z) avec k dans R.

Merci de poser des questions si besoin.

[arnaud32]

il te faut en fait montrer la continuite de f

[Anonyme]

il te faut en fait montrer la continuite de f

Voici cequ'on sait


avec
est bornée sur une partie de E d'intérieur non vide

Question : Comment déduire que avec

1)
R-linéaire veut il dire ou ?

2)
Est ce démontrer la continuité en z=0 uniquement suffit ?
ou
faut il démontrer la continuité en tout z de E ?

3)
Est ce que le fait d'être en dimension finie a une importance ?

4)
Pourquoi la continuité en 0 répondrait à cette question ?
C'est à dire comment déduire qu'à partir des hypothèses sur la fonction et à partir de :
tel que alors

que avec

[Exquise Sensation]

il te faut en fait montrer la continuite de f

Ui je pense avoir trouvé comment faire ça.

Déjà par hypothèse il existe a élément de E, M>0 et r>0 tq pour tout x de B(a,r), ||f(x)||0 tq pour tout k>0, il existe un élément de E x, tq ||x||E

Soit q un entier (ou rationnel peu importe) supérieur à M/E ( il est facile à trouver.. Floor(M/E)+1 par exemple!)
Pour k=r/(2q) il existe x dans E tq ||x||E

Or par construction qx appartient à B(0,r) et ||f(qx)||=||qf(x)||=q||f(x)||>qE
donc ||f(qx)||>M (car q>M/E) et qx est dans B(0,r).
Absurde. Donc f est continue en 0

Soit a élément de E soit (an) une suite d'élément de E convergeant vers a.
lim( f(an)-f(a) )=lim( f(an-a) )= f(0) = 0
car an-a -> 0 et f continue en 0 puis f(0+0)=f(0)+f(0)=> f(0)=0.
Donc f continue sur E et on conclut par densité de Q


Ce qui est étrange avec ma démo c'est que en remplaçant ma dernière phrase par un peu de travail je peu arriver au même résultat en remplaçant la Q-homogénéité par une N-homogénéité! ?

[Exquise Sensation]

Voici cequ'on sait


avec
est bornée sur une partie de E d'intérieur non vide

Question : Comme déduire que avec

1)
Est ce démontrer la continuité en z=0 uniquement suffit ?
ou
faut il démontrer la continuité en tout z de E ?

2)
Est ce que le fait d'être en dimension finie a une importance ?


3)
Pourquoi la continuité en 0 répond à cette question ?
C'est à dire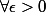
tel que alors

Ah ui la question B m'aurait permis de ne pas montrer la continuité sur tout E. On pouvait passer directement de la l'homogénéité en 0 à l'homogénéité sur E grâce à l'additivité? C'est ça.?

[arnaud32]

la premiere relation assure la continu partout si tu as la continuite en 0 car f(0)=0

[Exquise Sensation]

la premiere relation assure la continu partout si tu as la continuite en 0 car f(0)=0

Ui c'est comme ça que j'ai fait !

[Exquise Sensation]

Ce qui est étrange avec ma démo c'est que en remplaçant ma dernière phrase par un peu de travail je peu arriver au même résultat en remplaçant la Q-homogénéité par une N-homogénéité! ?

Si on remplace la Q-homogénéité par une N-homogénéité:
Tout roule jusqu'à ma dernière phrase qu'on remplace par:
Soit q=p/q (p,q) élément de NxN*
Soit z dans E
f(qz)=f( p(z/q) )=pf(z/q) car p est entier

or q!=0 donc f(z)=f( q(z/q) )=qf(z/q)
donc pf(z/q)=p/q f(z) et f est Q-homogène.
Par densité de Q et continuité de f, cette dernière est R linéaire

[Exquise Sensation]

Is it true? :we:

[arnaud32]

oui c'est vrai que tu as redondance entre ta premiere relation et la Q homogeneite