Une équation fonctionnelle TS

[Georges Leroy]

Si on veut résumer f est soit la fonction nulle, soit la fonction constante égale à 1 et aussi je dirai exp(kx) pr k réel

Oui, exactement !

Donc il faut que Ke^ax = 0
Ou Ke^ax=1
Ou Ke^ax = e^kx

J'ai essayé de résoudre ça et je ne vois pas vraiment ou ça mène..

[Rebelle_]

Bonsoir ! =)

Bon, je reviens à la charge avec ce que je disais tout à l'heure.... ;) Si f est une fonction non nulle et qu'elle transforme les sommes en produits alors elle est de la forme que je donnais ce matin.

Je suis tout à fait d'accord avec Nightmare : par théorème, la famille de fonctions exponentielles dont on a la forme est solution de l'équation fonctionnelle quelle que soit la valeur de K.
Ledit théorème est fondamental dans ce cours, tu as dû le voir ;)

[Mortelune]

Bonsoir,

5_A quelle condition sur K la fonction x-> est-elle solution de l'équation fonctionnelle ?

L'équation étant :
on doit donc avoir

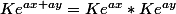
Ce qui donne bien une condition sur K comme tu semblais le décrire précédemment.

[Georges Leroy]

Bonsoir,


L'équation étant :
on doit donc avoir

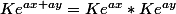
Ce qui donne bien une condition sur K comme tu semblais le décrire précédemment.

Bonsoir !

Je ne vois pas comment on continue =S

[Georges Leroy]

5_ Conclure.

Auriez vous une idée ? =S

[Georges Leroy]

Bonjour

Il me semble que les fonctions f non nulles et dérivables sur R telles que pour tous x et y réels f(x+y) = f(x)f(y) soient les fonctions x -> e^{kx} où k est un réel...
Comment le démontrer ?

La réponse finale était là !

En conclusion, les fonctions solutions sont les fonctions de la forme x -> e^{kx} où k est un réel

Merci beaucoup à tous !

[Zweig]

... et la fonction nulle

[LuffyChem]

Pourriez vous m'aidez également svp :/

http://www.maths-forum.com/dm-limites-suites-115749.php voici le lien pour mon DM.
Si jamais il marche pas allez dans le menu puis lycée et c'est DM limite et suite.
Help please :/

[sad13]

salut, En conclusion, les fonctions solutions sont les fonctions de la forme x -> e^{kx} où k est un réel

oui très bien mais on peut mieux dire pr être rigoureux :
f est : ->soit la fonction identiquement nulle (car K²=K donc K=0 ou 1)
->soit de la forme K*exp(ax) avec a réel (................................ )

et on retrouve bien le cas particulier f est la fonction constante égale à 1 si on prend a=0 .

Voilà . Bonne continuation

[Georges Leroy]

Effectivement, j'avais oublié la fonction nulle ! Et bien merci beaucoup à tous pour votre aide, ça m'avance pas mal ! Au delà d'avoir une bonne note, ce qui n'est pas négligeable vu mon niveau en mathématiques, je pense avoir bien compris les équations fonctionnelles et différentielles ! Merci :we:

[sad13]

je précise que la 1ère ligne était la citation de ta phrase et ce qui suit est le résumé final :
f est : ->soit la fonction identiquement nulle (car K²=K donc K=0 ou 1)
->soit de la forme K*exp(ax) avec a réel (................................ )

et on retrouve bien le cas particulier f est la fonction constante égale à 1 si on prend a=0 .

Courage et @bientôt