Equation fonctionnelle

par **instinct** » 21 Juil 2010, 15:17

Bonjour,
Est-ce que quelqu'un peut m'aider à résoudre cet exercice:

Soit f une fonction définie sur R et continue en 0, telle que :
f(x) = f(2x).
Montrer que f est constante sur R.

Merci.

par **girdav** » 21 Juil 2010, 15:26

Bonjour,
que donne la formule si tu itères la relation?

par **geegee** » 21 Juil 2010, 15:48

Bonjour,

f(x)=f(2x)=f(2nx) par récurrence avec n appartenant a

.

Donc pour tous x f(x) est constante.

par **girdav** » 21 Juil 2010, 15:54

Attention : par exemple

donc la relation est plutôt de la forme

(car "on multiplie par 2 à chaque fois").
Il faut de plus utiliser la continuité.

par **instinct** » 21 Juil 2010, 15:56

Oui geegee, f(x)=f(2x)=f(2^n * x), mais ça ne montre pas que f(x) = f(3x), par exemple. On ne sait pas si f(x) est toujours égale à f(0).

par **girdav** » 21 Juil 2010, 16:00

Si tu poses

, que devient la relation démontrée? Que se passe-t-il si

devient très grand?

par **instinct** » 21 Juil 2010, 16:04

Quand n est très grand, y est très grand, on a donc f(x) = f(y)
(x est petit et y est grand) mais ça ne résout pas le problème.

par **girdav** » 21 Juil 2010, 16:50

On a

pour tout entier n et pour tout réel y. Que vaut

?

par **geegee** » 21 Juil 2010, 16:57

En derivant a droite et a gauche on obtient que :

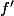
= 2

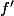
donc

donc f est constante

par **girdav** » 21 Juil 2010, 16:57

geegee a écrit:En derivant a droite et a gauche on obtient que :
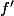
= 2
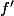
donc
donc f est constante

Comment montres-tu la dérivabilité?

par **Doraki** » 21 Juil 2010, 17:00

moi en dérivant j'ai pas f' = 2f', mais f'(x) = 2f'(2x)

par **geegee** » 21 Juil 2010, 17:11

et si on essayait de montrer que f(x)=f(2nx)=f(x/2n) pour tout entier n.
On veut montrer que f(x)=f(0) pour tout x, pour cela on va procéder en montrant que pour tout epsilon strictement positif |f(x)-f(0)|On pose alors un epsilon strictement positif. Par continuité de f en 0 il existe a strictement positif tel que si -a
Maintenant pour tout x réel, si n est suffisamment grand -a
Ps: cette solution est de s321
qu en pensez vous?

par **girdav** » 21 Juil 2010, 17:32

Ça marche et ça découle du fait plus général que si

est une fonction continue en

et

une suite qui converge vers x alors la suite

converge vers

. La démonstration est (presque) la même que celle que tu viens de faire.

par **instinct** » 21 Juil 2010, 17:55

Merci Girdav,
C'est donc :

f(x)=f(2^n *x)

f(y/2^n)=f(y), avec y = x * 2^n

f(y) = f(0) (quand n est grand, quel que soit y)

par **mathelot** » 21 Juil 2010, 18:31

Bonsoir,

pour tout x,

pour tout n

en passant à la limite

quelque soit x.

par **geegee** » 21 Juil 2010, 18:32

Desole pour ces tentatives...

Equation fonctionnelle

Equation fonctionnelle

Qui est en ligne