Encadrer une intégrale

[Kiwiks]

Bonjour,

Je n'arrive pas à montrer que est bornée. Je pensais utiliser le fait que cos est compris en t et -t mais ça me donne une majoration et une minoration qui dépendent de t...

Est ce que quelqu'un pourrait m'aider ?

Je vous remercie!

[Actéon]

As-tu essayé d'autres pistes déjà? La comme ça je dirais, mais je ne garantis pas, à toi de vérifier, pourquoi pas écrire cos(x^2) = x cos(x^2)/x puis tenter une IPP?
(il faudra peut-etre, au moment de la majoration ,distinguer le voisinage de 0 du voisinage de l'infini)
on peut penser aussi au changement de variable, essaie mais je pense pas que ça marche bien.

[Kiwiks]

D'accord merci! J'essaye

[girdav]

En fait tout se ramène à montrer que est borné. Si on pose (donc ) on obtient que puis on peut faire une intégration par parties.

[Pythales]

On peut montrer que

mais c'est un peu long ...

[Actéon]

On peut montrer que

mais c'est un peu long ...

lol je ne pense pas en effet que ce soit ce qui est demandé!
Le changement de variable, il faut effectivement que ça fasse "tilt" dans une situation comme ça, il faut le retenir. Mais là je crois qu'on peut s'en passer en multipliant artificiellement par x/x, comme je t'ai proposé. Tu nous diras...

[buzard]

Bonsoir,

Tu peux utiliser la formule de Moivre, pour ramener l'intégrale à une exponentielle complexe, que tu compare avec des intégrales connus. C'est pas évident, mais ça se fait.

dis nous si tu bloque encore.

[Kiwiks]

Merci beaucoup pour toutes vos indications ! comme j'ai un cerveau très lent :hum: je risque de prendre du temps avant de trouver alors quand je trouve quelque chose je vous en ferai part ! :lol3:

[buzard]

Merci beaucoup pour toutes vos indications ! comme j'ai un cerveau très lent :hum: je risque de prendre du temps avant de trouver alors quand je trouve quelque chose je vous en ferai part ! :lol3:

Si tu cherche des référence, regarde du côtés des fonctions et intégrales de Fresnel.

[arnaud32]

tu peux faire un changement de variables
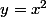
tu vas avoir une integrale en
que tu vas regarder sur les interevalles du type et
sur chaque intervalle le cos a un signe constant
tu peux encadrer avec les bornes de l'intervalle, multiplier par cos(y) et integrer.
tu vas ainsi encadrer ton integrale entre deux serries ...

[Pythales]

Je reconnais que "ma" formule est un peu compliquée. La démo prend une demi page environ.
Elle a quand même 2 avantages :
- elle ne fait pas du tout appel aux complexes
- elle permet de calculer les intégrales de Fresnel (Il existe une formule similaire pour le sinus).

[Kiwiks]

Bonsoir !

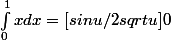
Ce que j'ai fait: j'ai intégré par partie et j'ai trouvé que0 à t [TEX] + 1/4 * C sinu/u^3/2[/TEX

L'intégrale tout à droite <= à

[Kiwiks]

Bonsoir !

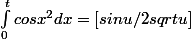
Ce que j'ai fait: j'ai intégré par partie et j'ai trouvé que0 à t

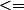
L'intégrale tout à droite à et j'ai prouvé que cette intégrale converge. Il me reste mais je n'arrive pas à borner ce terme parce que t intervient toujours...

C'est bon jusqu'à là ce que je dis ?

[Ben314]

Oui, c'est bon et quand à ça :

...Il me reste mais je n'arrive pas à borner ce terme parce que t intervient toujours...

il n'y a pas de problème : ta fonction (de u) est continue, y compris en 0 et elle tend vers 0 en +oo et en -oo : elle set donc bornée sur R.

[Kiwiks]

Ce veut dire que toute fonction continue sur R et qui converge en + et - l'infinie est bornée ?
L'année dernière je n'avais vu ça que sur un segment

[Ben314]

Ce veut dire que toute fonction continue sur R et qui converge en + et - l'infinie est bornée ?
L'année dernière je n'avais vu ça que sur un segment

Ben si elle admet une limite L en -oo alors elle est entre L-1 et L+1 pour tout x plus petit qu'un certain M.
De même si elle admet une limite L' en +oo alors elle est entre L'-1 et L'+1 pour tout x plus grand qu'un certain M'.
Enfin, entre M et M', ben c'est une fonction continue sur le segment [M',M] donc elle est bornée...